Практическое занятие по теме «Векторные пространства-1»

Практическое занятие по теме «Векторные пространства-1»

1. Проверить, является ли векторным пространством над полем действительных чисел множество квадратных матриц 2-го порядка 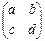, 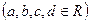относительно операций сложения и умножения на число.

2. Проверить, является ли векторным пространством над полем действительных чисел множество линейных многочленов с действительными коэффициентами относительно операций сложения и умножения на число.

3. Является ли векторным пространством множество V всех векторов- решений однородной системы линейных уравнений с n переменными? Что является базисом этого пространства? Подпространством какого пространства является множество V?

4.Пусть L – линейное пространство всех вещественных квадратных матриц порядка n с действительными элементами над полем R и 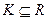. Является ли K подпространством, если:

1) K – множество всех диагональных матриц;

2) K – множество всех невырожденных матриц;

3) K – множество всех матриц, у которых первая строка состоит из 0.

5.Является ли подпространством векторного пространства векторов плоскости над полем R множество векторов плоскости, концы которых лежат:

а) в 1 четверти системы координат;

б) в 1 или 3 четвертях системы координат ?

6. Найти линейную комбинацию арифметических векторов:

а) 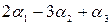, если , , ;

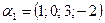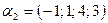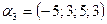б) 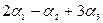, если , , .

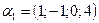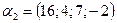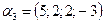7. Будет ли данная система векторов линейно зависимой:

а) , , ;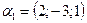

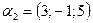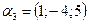б) , , ;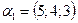

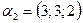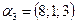в) , , , ?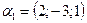

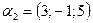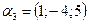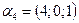8. Доказать: а) система векторов, содержащая два равных вектора, линейно зависима; б) система векторов, два вектора которой различаются скалярным множителем, линейно зависима.

Литература

1. Вечтомов Е.М., Лубягина Е.Н. Курс линейной алгебры: учебное пособие / Е.М. Вечтомов, Е. Н. Лубягина. 2-e изд., изм. — Киров: ВятГУ, ООО «Веси», 2019. 177 с.

2. Подлевских, М.Н.Линейная алгебра: учебно-методическое пособие / М.Н.Подлевских.- Киров: ПРИП ФГБОУ ВПО «ВятГУ», 2013.- 37 с.