Хелпикс

Главная

Контакты

Случайная статья



Примерные!!!  практические задания для экзамена.

Стр 1 из 2Следующая ⇒


Примерные!!!  практические задания для экзамена.

ТЕМА1. Матрицы. Определители. Решение СЛАУ. Векторная алгебра. Аналитическая геометрия на плоскости и в пространстве.

 

ЗАДАЧА №1.

Известны точки А(2,3,-2) ,В(2,0,7), C(3,4,1), D(5,1,9).Найти проекцию вектора AC на направление , задаваемое вектором ВD.

ЗАДАЧА №2.

Известны точки А(0,2,-2) ,B(2,0,4) ,C(4,3,6).Найти площадь треугольника АВС и его высоту .

 

ЗАДАЧА №3.

Установить , можно ли через точки A(2,2,-2), B(2,3,1), C(2,4,-1) и D(3,-2,5) провести плоскость .

 

ЗАДАЧА №4. Решить СЛАУ методом Крамера, методом Гаусса, с помощью обратной матрицы.

 

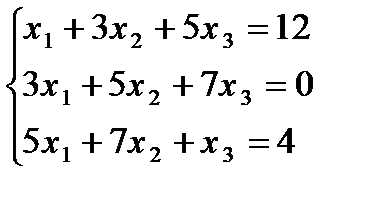
ЗАДАЧА №5 Найти 2F-AB , где A=      B=   F=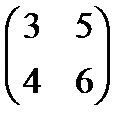

 

ЗАДАЧА №6.

Найти длины диагоналей параллелограмма , построенного на векторах

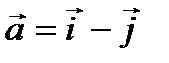 и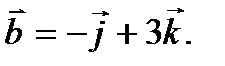

 

ЗАДАЧА №7.

Известны точки А(1,1,-2) ,B(2,4,-3) , C(2,1,-1) ,D(3,2,0) .Найти угол между векторами AB и DC.

 

ЗАДАЧА №8.

Угол между векторам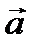и и 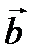 равен 450. Найти площадь параллелограмма, построенного на векторах 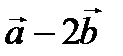и 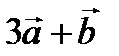, если ,

 

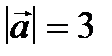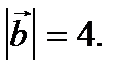
ЗАДАЧА №9

Определить и построить вектор если

 

ЗАДАЧА №10.

Найти значение ,при котором векторы  и 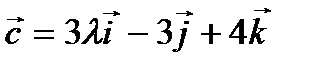компланарны.

 

ЗАДАЧА №11.

Найти объем параллелепипеда , построенного на векторах 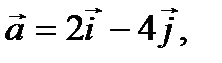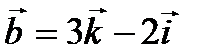и  как на сторонах.

 

ЗАДАЧА №12.

Даны три вершины треугольника АВС – точки А, В, и С, А(2;5), В(4;-2), С(-5,3).

1) составить уравнения сторон АВ, ВС и АС,

2) найти точку пересечения высот треугольника АВС,

3) найти точку пересечения медиан треугольника АВС,

4) найти длину высоты ВК,

5) найти внутренний угол треугольника при вершине В.

6) сделать чертеж в декартовой системе координат.

 

ЗАДАЧА №13.

Даны координаты вершин пирамиды :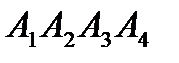

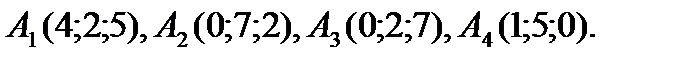
Найти:

1) длину ребра ,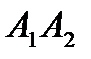

2) угол между ребрами ,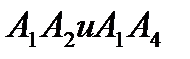

3) угол между ребром 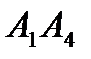 и гранью ,

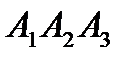4) канонические и параметрические уравнения прямой ,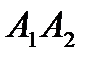

5) уравнение плоскости ,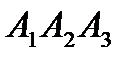

6) уравнения высоты, опущенной из вершины 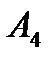 на грань .

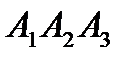7) длину высоты, опущенной из вершины 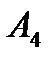 на грань .

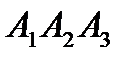8) проекцию вершины 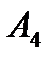 на плоскость .

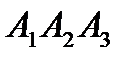9) сделать чертеж.



12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.