Обработка данных пассивного эксперимента»

Задание на лабораторную работу №3

«Обработка данных пассивного эксперимента»

Решить задачи параметрической и структурной идентификации эмпирической модели, описывающей зависимость давления насыщенного пара индивидуального вещества от температуры*.

При этом используются данные пассивного эксперимента (10 экспериментов), приведенные на отдельном листе с номерами вариантов, и 5 видов указанных моделей:

(1)** Р=ехр(А + В/Т)

(2) Р=ехр(А + В/(С+Т))

(3) Р=ехр(А + ВТ + СТ²)

(4) P=exp(A + B/T + CT + D lnT)

(5) Р=ехр(А + ВТ + СТ² + DТ³),

где А, В, С, D – определяемые коэффициенты**

а) Определить коэффициенты уравнений регрессии указанных 5 эмпирических моделей. Представить в общем и в числовом виде произведение транспонированной 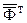и исходной 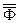матриц независимых входных переменных и числовые значения обратной матрицы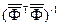

б) Определить адекватность уравнений регрессии с использованием F-распределения Фишера и
выбрать наиболее точное уравнение с использованием дисперсии адекватности. Расчётное
значение критерия Фишера в отсутствии параллельных опытов определяется по формуле:

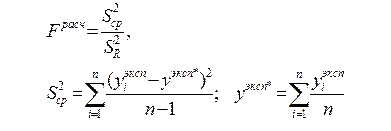
Условие адекватности: F^расч> F^табл.

Представить сводную таблицу коэффициентов А, В, С, D, дисперсий, табличных и расчётных критериев Фишера для всех моделей. Выделить наиболее точную модель.

в) Линеаризованные уравнения преобразовать, выразив выходную переменную и построить графики ошибок для каждого уравнения (график ошибок – график разностей экспериментальных и расчётных значений в зависимости от значения аргумента). Подобрать масштаб оси ординат позволяющий подробно рассмотреть форму кривой на графике.

г) Провести графическое сравнение экспериментальных и расчетных данных.

д) Сформулировать выводы по работе.

(* – Не переводить в другую размерность)

(** – Не менять порядок коэффициентов и номера зависимостей, не менять обозначений)