Заведующий каф. НГ и Г проф. Бобин Н. Е.
| №
| вопрос
| варианты ответов
| |
| В каком октанте расположена точка А?
| 1. в 1-м октанте;
2. в 2-м октанте;
3. в 3-м октанте;
4. в 4-м октанте;
5. в 5-м октанте.
| |
| Построить третью проекцию точки А (укажите верный ответ):
| 1) 2)
3) 4)
5)
| |
| В каком октанте расположена точка А?
| 1. в 1-м октанте;
2. в 2-м октанте;
3. в 3-м октанте;
4. в 4-м октанте;
5. в 5-м октанте
| |
| В каком октанте расположена точка А?
| 1. в 5-м октанте;
2. в 6-м октанте;
3. в 7-м октанте;
4. в 8-м октанте;
5. в 4-м октанте.
| |
| Построить точку М / - горизонтальный след прямой АВ:
| 1. точка 1;
2. точка 2;
3. точка 3;
4. точка 4;
5. точка 5.
| |
| Как называется прямая 1 -В?
| 1. фронталь плоскости Δ АВС;
2. горизонталь плоскости Δ АВС;
3. профильная прямая плоскости Δ АВС;
4. линия наибольшего ската плоскости Δ АВС;
5. прямая общего положения.
| |
| В каком октанте расположена точка А?
| 1. в 1-м октанте;
2. в 2-м октанте;
3. в 6-м октанте;
4. в 7-м октанте;
5. в 8-м октанте.
| |
| Какая точка соответствует фронтальному следу прямой АВ?
| 1. точка 4;
2. точка 3;
3. точка 2;
4. точка 5;
5. точка 1.
| |
| Какое положение относительно горизонтальной плоскости проекций p1 занимает горизонтально - проецирующая прямая?
| 1. параллельна плоскости p1;
2. перпендикулярна плоскости p1;
3. расположена под углом 450 к плоскости p1;
4. расположена под любым углом к плоскости p1;
5. лежит в плоскости p1.
| |
| В каком октанте расположена точка А?
| 1. в 1-м октанте;
2. в 5-м октанте;
3. в 6-м октанте;
4. в 7-м октанте;
5. в 8-м октанте
| |
| Что является следом прямой?
| 1. любая точка прямой;
2. проекция любой точки прямой на плоскость проекций;
3. точка прямой, лежащая в плоскости проекций;
4. проекция прямой на плоскость проекций;
5. проекция прямой на горизонтальную плоскость проекций.
| |
| Как называется прямая 1 -С?
| 1. фронталь плоскости Δ АВС;
2. горизонталь плоскости Δ АВС;
3. профильная прямая плоскости Δ АВС;
4. линия наибольшего ската плоскости Δ АВС;
5. прямая общего положения.
| |
| Что является следом плоскости?
| 1. точка в плоскости;
2. проекция прямой, лежащей в плоскости, на любую плоскость проекций;
3. линия пересечения плоскости с плоскостью проекций;
4. любая прямая, лежащая в плоскости;
5. прямая, пересекающая плоскость.
| |
| По двум заданным проекциям укажите горизонталь плоскости Δ АВС:
| 1. прямая «А3»;
2. прямая «В2»;
3. прямая «С3»;
4. ни одна из прямых на чертеже не является горизонталью Δ АВС;
5. прямая «СВ».
| |
| Какое минимальное количество следов плоскости на чертеже определяют ее положение в пространстве?
| 1. любой один из следов;
2. горизонтальный след;
3. фронтальный след;
4. любые два следа;
5. профильный след.
| |
| Как расположена относительно осей координат линия пересечения плоскостей a и b?
| 1. параллельна оси ОУ;
2. параллельна оси ОZ;
3. перпендикулярна оси ОХ;
4. параллельна оси ОХ;
5. совпадает с осью ОХ.
| |
| Укажите плоскости частного положения:
1) 2) 3)
4) 5)
| 1. плоскости варианты 1 и 2;
2. плоскости варианты 2 и 3;
3. плоскость вариант 4;
4. плоскости варианты 1, 2 и 4;
5. плоскости варианты 2, 3 и 5.
| |
| По двум заданным проекциям укажите фронталь плоскости Δ АВС:
| 1. прямая «А3»;
2. прямая «В2»;
3. прямая «С3»;
4. ни одна из прямых на чертеже не является фронталью Δ АВС;
5. прямая «АВ».
| |
| Выберите совокупность действий для построения точки пересечения прямой АВ с заданной плоскостью a.
| 1. найти следы прямой;
2. заключить прямую во вспомогательную плоскость b;
3. построить линию пересечения вспомогательной плоскости b с заданной плоскостью a;
4. определить истинную величину отрезка АВ;
5. выполнить действия по пунктам 2, 3 и найти точку пересечения прямой с линией пересечения плоскостей a и b.
| |
| Укажите горизонтально – проецирующую плоскость:
1) 2) 3)
4) 5)
| 1. плоскость 1-й вариант;
2. плоскость 2-й вариант;
3. плоскость 3-й вариант;
4. плоскость 4-й вариант;
5. плоскость 5-й вариант.
| |
| Какие признаки соответствуют плоскости частного положения: 1 – не параллельна ни одной из координатных осей;
2 – пересекает ось ОХ под углом 450 и перпендикулярна фронтальной плоскости проекций p2;
3 – расположена под острым углом ко всем плоскостям проекций;
4 – параллельна одной из плоскостей проекций;
5 – перпендикулярна одной из плоскостей проекций.
| 1. признаки по п.1;
2. признаки по п.2;
3. признаки по п.п.2 и 4;
4. признаки по п.п.2, 4 и 5;
5. признаки по п.п. 4 и 5.
| |
| Укажите фронтально – проецирующую плоскость:
1) 2) 3)
4) 5)
| 1. плоскость 1-й вариант;
2. плоскость 2-й вариант;
3. плоскость 3-й вариант;
4. плоскость 4-й вариант;
5. плоскость 5-й вариант.
| |
| Какое положение в пространстве должен занять отрезок прямой АВ, чтобы его фронтальная проекция соответствовала бы его истинной величине?
| 1. должен быть параллелен горизонтальной плоскости проекций p1;
2. должен быть параллелен горизонтальной плоскости проекций p2;
3. должен быть параллелен горизонтальной плоскости проекций p3;
4. должен быть направлен к точке начала координат;
5. произвольное положение.
| |
| Какое положение плоскостей a и b в пространстве?
| 1. профильно - проецирующие плоскости;
2. общего положения;
3. горизонтальные плоскости;
4. фронтальные плоскости;
5. профильные плоскости.
| |
| Является ли плоскость g плоскостью общего положения при условии, что она проходит через ось ОХ ?
| 1. да, является;
2. является плоскостью частного положения;
3. да, является только в пределах I октанта;
4. да, является только в пределах III октанта;
5. да, является везде, кроме I и III октантов.
| |
| Какой вариант из предложенных соответствует правильному построению проекций линии пересечения плоскостей a и b?
1) 2)
2) 4)
5)
| 1. 1-й вариант;
2. 5-й вариант;
3. 2-й вариант;
4. 3-й вариант;
5. 4-й вариант.
| |
| По двум заданным проекциям прямых и следам плоскости a укажите прямую, лежащую в этой плоскости:
| 1. прямая a;
2. прямая b;
3. прямая c;
4. прямая d;
5. прямая e.
| |
| Укажите варианты, соответствующие параллельным плоскостям:
1) 2)
3) 4)
5)
| 1. только 2-й вариант;
2. только 3-й вариант;
3. 2-й и 3-й варианты;
4. 2-й, 3-й и 5-й варианты;
5. только 4-й вариант.
| |
| Какой вариант из предложенных соответствует правильному построению горизонтально - проецирующей плоскости, проходящей через прямую АВ?
1) 2)
3) 4)
5)
| 1. 5-й вариант;
2. 3-й вариант;
3. 2-й вариант;
4. 1-й вариант;
5. 4-й вариант.
| |
| Какой вариант из предложенных соответствует правильному построению фронтально - проецирующей плоскости, проходящей через прямую АВ?
1) 2)
3) 4)
5)
| 1. 1-й вариант;
2. 2-й вариант;
3. 3-й вариант;
4. 4-й вариант;
5. 5-й вариант.
| |
| Какие варианты заданных плоскостей соответствуют плоскости общего положения?
1) 2) 3)
4) 5)
| 1. плоскости варианты 1 и 2;
2. плоскости варианты 2 и 3;
3. плоскость вариант 4;
4. плоскости варианты 1, 2 и 4;
5. плоскости варианты 2, 3 и 5.
| |
| Какое положение в пространстве занимает отрезок АВ, если горизонтальная проекция отрезка соответствует его истинной величине?
| 1. параллелен плоскости p1;
2. параллелен плоскости p2;
3. параллелен плоскости p3;
4. перпендикулярен плоскости p1;
5. произвольное положение.
| |
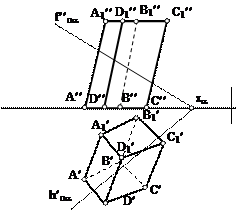
| Через какие октанты проходит прямая АВ?
| 1. прямая проходит через I, II, III и VII октанты;
2. прямая проходит через II, I, V и VIII октанты;
3. прямая проходит через III, IV, VIII и V октанты;
4. прямая проходит через II, VI, VII и VIII октанты;
5. прямая проходит через III, IV, VI и VII октанты;
| |
| В каком случае истинная величина отрезка АВ определена верно?
1) 2)
3) 4)
5)
| 1. 1-м случае;
2. 2-м случае;
3. 3-м случае;
4. 4-м случае;
5. 5-м случае.
| |
| В каком октанте расположена точка А, принадлежащая прямой АВ?
| 1. в I-м октанте;
2. во II-м октанте;
3. в V-м октанте;
4. в VI-м октанте;
5. в VIII-м октанте.
|  36 36
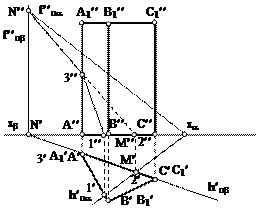
| На каком эпюре правильно указан угол наклона прямой АВ к горизонтальной плоскости проекций p1?
1) 2)
3) 4)
5)
| 1. 1-й эпюр;
2. 2-й эпюр;
3. 3-й эпюр;
4. 4-й эпюр;
5. 5-й эпюр.
| |
| Какой вариант из предложенных соответствует правильному построению проекций линии пересечения плоскостей a и b?
1) 2)
3) 4)
5)
| 1. 1-й вариант;
2. 2-й вариант;
3. 3-й вариант;
4. 4-й вариант;
5. 5-й вариант.
| 
| №
| вопрос
| варианты ответов
| |
| Какой способ проецирования дает наиболее наглядное изображение предмета?
| 1. косоугольный
2. параллельный
3. перспективный
4. ортогональный
5. центральный
| |
| Какой способ проецирования применён при проецировании точки А на плоскость p0?
| 1. косоугольный
2. параллельный
3. перспективный
4. ортогональный
5. центральный
| |
| Какой способ проецирования применён при проецировании точки С на плоскость p0?
| 1. косоугольный
2. параллельный
3. перспективный
4. ортогональный
5. центральный
| |
| Как обозначается проекция точки А на плоскость, если проецирующая прямая параллельна этой плоскости?
| 1. А¢
2. А²
3. А¢¢¢
4. А0
5. Аµ
| |
| Какие плоскости проекций являются основой метода Монжа?
| 1. p1
2. p2
3. p3
4. p1p2
5. p1p2p3
| |
| Какое положение в системе p1,p2 должна занять новая плоскость проекций p3, вводимая для образования системы p3,p1?
| 1. p3 || p1
2. p3 ^ p1
3. p3 ^ p2
4. p3 || p2
5. p3 || ох
|
| №
| вопрос
| варианты ответов
| |
| Какое положение займет новая плоскость проекций p4 при определении угла наклона прямой АВ к плоскости проекций p1?
| 1. p4 || АВ
2. p4 ^ АВ
3. p4 Ç АВ
4. p4 || ох
5. p4 ^ ох
| |
| Какое положение займет новая плоскость проекций p4 при определении угла наклона прямой АВ к плоскости проекций p2?
| 1. p4 || АВ
2. p4 ^ АВ
3. p4 Ç АВ
4. p4 || ох
5. p4 ^ ох
| |
| Какое положение займет новая плоскость проекций p4 при определении расстояния между двумя параллельными плоскостями a и b?
| 1. p4 || ох
2. p4 || оу
3. p4 || оz
4. p4 ^ a || b
5. p4 || a || b
| |
| Сколько новых плоскостей проекций необходимо ввести для определения угла между двумя пересекающимися плоскостями общего положения?
| 1. одну
2. две
3. три
4. ни одной
5. сколько угодно
| |
| Какое положение займет новая фронтальная плоскость проекций p4 для того, чтобы плоскость a в новой системе p1,p4 оказалась фронтально-проецирующей?
| 1. p4 || a
2. p4 || ох
3. p4 || оу
4. p4 ^ a
5. p4 || oz
| |
| Сколько новых плоскостей проекций необходимо ввести для определения истинной величины плоской фигуры общего положения?
| 1. одну
2. две
3. три
4. ни одной
5. сколько угодно
| |
| Какая координата точки при введении новой плоскости проекций p4 ^ p1 будет одинаковой для системы p1, p2 и p1, p4?
| 1. по оси Х
2. по оси У
3. по оси Z
4. все
5. ни одна
| |
| Какая из этих плоскостей не может быть новой плоскостью проекций?
| 1. горизонтально - проецирующая
2. фронтально - проецирующая
3. горизонтальная
4. фронтальная
5. общего положения
|
| №
| вопрос
| варианты ответов
| |
| Сколько новых плоскостей проекций необходимо ввести для определения истинной длины отрезка прямой АВ?
| 1. одну
2. две
3. три
4. ни одной
5. сколько угодно
| |
| При использовании метода вращения, что меняет своё положение в пространстве?
| 1. горизонтальная плоскость проекций p1;
2. фронтальная плоскость проекций p2;
3. плоскости проекций p1, p2, p3;
4. объект;
5. объект и плоскость вращения.
| |
| Что такое плоскость вращения?
| 1. горизонтальная плоскость проекций p1;
2. фронтальная плоскость проекций p2;
3. плоскость, в которой перемещается объект вращения вокруг оси вращения;
4. любая горизонтальная плоскость;
5. любая плоскость.
| |
| Как плоскость вращения располагается по отношению к оси вращения?
| 1. перпендикулярно к оси вращения;
2. под любым углом к оси вращения;
3. независимо от оси вращения, но параллельно p1;
4. независимо от оси вращения, но параллельно p2;
5. параллельно оси вращения.
| |
| Где находится центр вращения точки при повороте её вокруг некоторой оси?
| 1. в любой точке плоскости p1;
2. в любой точке плоскости p2;
3. в точке пересечения оси вращения с плоскостью вращения;
4. в любой точке плоскости вращения;
5. в плоскости вращения по построению.
| |
| Основные элементы метода вращения?
| 1. объект вращения, ось вращения, плоскость вращения, центр вращения, радиус вращения;
2. ось вращения, радиус вращения, объект вращения;
3. объект вращения, ось вращения, плоскость вращения;
4. объект вращения, ось вращения, центр вращения, радиус вращения;
5. объект вращения, ось вращения;
| | №
| вопрос
| варианты ответов
| |
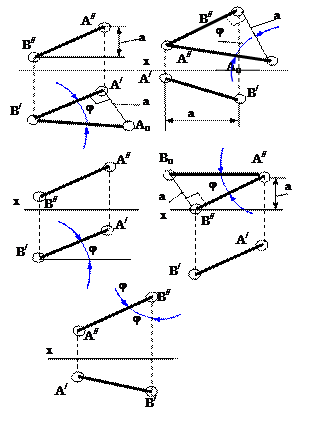
| Точка вращается вокруг оси ^ плоскости проекций p1.
Как перемещается её горизонтальная проекция?
| 1. по линии || ОХ;
2. по линии || ОУ;
3. по окружности с произвольным центром;
4. по окружности, центром которой является проекция оси вращения на плоскость;
5. по произвольной кривой.
| |
| Точка вращается вокруг оси ^ плоскости проекций p1.
Как перемещается её фронтальная проекция?
| 1. по линии || ОХ;
2. по линии || ОУ;
3. по окружности с произвольным центром;
4. по окружности, центром которой является проекция оси вращения на плоскость;
5. по произвольной кривой.
| |
| Точка вращается вокруг оси ^ плоскости проекций p2.
Как перемещается её горизонтальная проекция?
| 1. по линии || ОХ;
2. по линии || ОУ;
3. по окружности с произвольным центром;
4. по окружности, центром которой является проекция оси вращения на плоскость;
5. по произвольной кривой.
| |
| Точка вращается вокруг оси ^ плоскости проекций p2.
Как перемещается её фронтальная проекция?
| 1. по линии || ОХ;
2. по линии || ОУ;
3. по окружности с произвольным центром;
4. по окружности, центром которой является проекция оси вращения на плоскость;
5. по произвольной кривой.
| |
| Как перемещается точка прямой, лежащая на оси вращения, ^ плоскости проекций p1?
| 1. по линии || ОХ;
2. по линии || ОУ;
3. по окружности;
4. не меняет своего положения;
5. но произвольной кривой.
| |
| Прямая АВ повёрнута вокруг оси, ^ плоскости p1, на угол j.
На какой угол будут повёрнуты горизонтальные проекции точек А и В?
| 1. на угол j¢А и угол j¢В;
2. на угол j¢А;
3. на угол j¢В;
4. на угол < угла j;
5. на угол j.
| |
| Вокруг какой оси надо повернуть прямую АВ, чтобы получить её истинную величину во фронтальной плоскости проекций p2?
| 1. оси, ^ плоскости p1;
2. оси, ^ плоскости p2;
3. оси, || плоскости p1;
4. оси, || плоскости p1 и p3;
5. произвольной оси.
| | №
| вопрос
| варианты ответов
| |
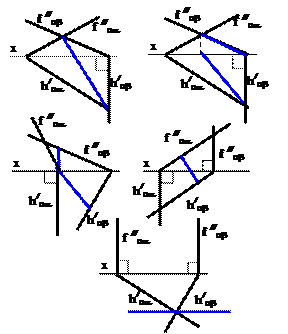
| Вокруг какой оси надо повернуть прямую АВ, чтобы получить её истинную величину во фронтальной плоскости проекций p2?
| 1. оси, ^ плоскости p1;
2. оси, ^ плоскости p2;
3. оси, || плоскости p1;
4. оси, || плоскости p1 и p3;
5. ороизвольной оси.
| |
| Какая из проекций отрезка прямой линии при вращении вокруг оси, ^ плоскости p1, не изменяет своей величины?
| 1. фронтальная проекция;
2. горизонтальная проекция;
3. профильная проекция;
4. фронтальная и горизонтальная проекции;
5. все проекции меняют свою величину.
| |
| Как называется метод вращения, при котором оси вращения, ^ плоскости p1 и плоскости p2 не указываются, а проекции точек допускается перемещать в плоскостях их вращения на свободное поле чертежа?
| 1. метод свободного вращения;
2. метод плоскопараллельного перемещения;
3. метод совмещения;
4. метод вращения и перемещения;
5. комбинированный метод вращения.
| |
| Вокруг какой оси надо повернуть плоскость треугольника, чтобы его плоскость стала фронтально проецирующей?
| 1. вокруг оси, ^ плоскости p1;
2. вокруг оси, ^ плоскости p2;
3. вокруг оси, || плоскости p1;
4. вокруг осей, || плоскости p1 и p2;
5. вокруг любой оси.
| |
| В каком случае не изменяется при вращении наклон прямой линии по отношению к плоскости p3?
| 1. вокруг оси, ^ плоскости p1;
2. вокруг оси, ^ плоскости p2;
3. вокруг оси, ^ плоскости p3;
4. вокруг оси, || плоскости p1;
5. вокруг любой оси.
| |
| Путём поворота вокруг какой оси можно определить длину отрезка прямой линии и угол её наклона к плоскости p1?
| 1. поворотом вокруг оси, ^ пл. p1;
2. поворотом вокруг оси, ^ пл. p2;
3. поворотом вокруг оси, ^ пл. p3;
4. поворотом вокруг оси, || пл. p1;
5. поворотом вокруг оси, || пл. p2;
| |
| Вращением, вокруг какой оси можно получить истинную величину плоской фигуры общего положения?
| 1. вокруг оси, ^ плоскости p1;
2. вокруг оси, ^ плоскости p2;
3. вокруг оси, || плоскости p1;
4. вокруг горизонтали плоской фигуры;
5. вокруг любой оси, || пл. p2.
|
| №
| вопрос
| варианты ответов
| |
| Какому методу присуще совмещение заданной плоскости и расположенных в ней геометрических элементов с соответствую- щими плоскостями проекций?
| 1. методу вращения вокруг оси, ^ плоскости проекций;
2. методу вращения вокруг оси, || плоскости проекций;
3. методу вращения вокруг следа заданной плоскости;
4. методу плоскопараллельного перемещения;
5. вращению вокруг любой оси.
| |
| Как называется метод вращения вокруг следа заданной плоскости?
| 1. метод вращения вокруг оси, ^ плоскости проекций;
2. метод вращения вокруг горизонтали;
3. метод вращения вокруг фронтали;
4. метод совмещения;
5. метод плоскопараллельного перемещения.
| |
| Какие элементы должны быть заданы для определения истинной величины фигуры, лежащей в плоскости, с помощью метода совмещения?
| 1. следы плоскости и две проекции фигуры;
2. один из следов плоскости и одна проекция фигуры;
3. два следа плоскости и одна проекция фигуры;
4. все следы плоскости и точка привязки фигуры;
5. два следа плоскости и точка привязки фигуры.
| |
| Какие элементы должны быть заданы для построения проекций фигуры, лежащей в плоскости, с помощью метода совмещения?
| 1. следы плоскости и истинная величина фигуры;
2. два следа плоскости, истинная величина фигуры и точка привязки фигуры к плоскости;
3. два следа плоскости и истинная величина фигуры;
4. три следа плоскости и истинная величина фигуры;
5. след плоскости, ось вращения, истинная величина фигуры и одна проекция точки привязки фигуры к плоскости.
|
| №
| вопрос
| варианты ответов
| |
| Плоский угол проецируется на горизонтальную плоскость проекции p1 без искажения, если:
| 1. плоский угол является плоскостью общего положения;
2. плоский угол является горизонтально – проецирующей плоскостью;
3. плоский угол || горизонтальной плоскости проекций p1;
4. плоский угол || фронтальной плоскости проекций p2;
5. плоский угол является фронтально – проецирующей плоскостью;
| |
| Какие плоские углы, являющиеся плоскостями общего положения, проецируются на плоскости проекций без искажения?
| 1. если плоскость угла является горизонтально – проецирующей плоскостью;
2. если плоскость угла является фронтально – проецирующей плоскостью;
3. если плоскость угла является любой проецирующей плоскостью;
4. прямой угол, катет которого параллелен плоскости проекций;
5. никакие.
| |
| Когда прямой угол, плоскость которого является плоскостью общего положения, проецируется на плоскость проекций без искажения?
| 1. всегда;
2. если один из катетов параллелен плоскости проекций;
3. всегда с искажением;
4. если плоскость угла ^ плоскости проекций p1;
5. если плоскость угла ^ плоскости проекций p2;
|
| №
| вопрос
| варианты ответов
| |
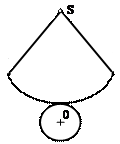
| Положение вспомогательной секущей плоскости a относительно плоскостей проекций.
| 1. горизонтально – проецирующая плоскость;
2. плоскость общего положения, проходящая через ось цилиндра;
3. фронтально – проецирующая плоскость;
4. плоскость общего положения, параллельная оси цилиндра;
5. осевая плоскость.
|  80 80
| Какая фигура получается в результате пересечения вспомогательной секущей плоскости a с поверхностью цилиндра?
| 1. окружность;
2. треугольник;
3. эллипс;
4. четырёхугольник;
5. трапеция.
|  81 81
| С какими гранями пирамиды пересекается прямая LT?
| 1. SCA и SAB;
2. ABC и SCA;
3. SCB и ABC;
4. SCB и SCA;
5. SCB и SAB.
|  82 82
| Положение прямой LT относительно геометрического тела АВСС1В1А1.
| 1. пересекает грани АВВ1А1 и АСС1А1;
2. пересекает грани ВСС1В1 и АВВ1А1;
3. пересекает грани АВС и А1В1С1;
4. не пересекает поверхность призмы;
5. пересекает грани ВСС1В1 и АСС1А1.
|
| №
| вопрос
| варианты ответов
| |
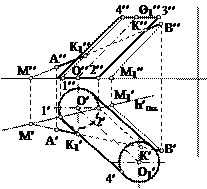
| По какой формуле определяется угол a при построении развёртки боковой поверхности прямого конуса?
| 1. a = 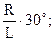 2. a =
2. a = 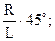 3. a =
3. a = 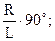 4. a =
4. a = 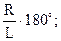 5. a =
5. a = 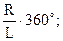 где R – радиус основания конуса?
L – длина образующих конуса.
где R – радиус основания конуса?
L – длина образующих конуса.
| |
| Каким способом определяется истинная длина образующих прямого конуса при построении его развёртки?
| 1. способом прямоугольного треугольника;
2. способом вращения;
3. способом перемены плоскостей проекций;
4. способом плоско–параллельного перемещения;
5. определять не надо.
| |
| Какой способ следует применять при определении истинной длины рёбер наклонной пирамиды при построении её развёртки?
| 1. способом прямоугольного треугольника;
2. способом вращения;
3. способом перемены плоскостей проекций;
4. способом плоско–параллельного перемещения;
5. никакой.
| |
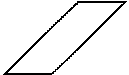
| Развёртка полной поверхности какого геометрического тела изображена на рисунке?
| 1. конуса;
2. цилиндра;
3. наклонной призмы;
4. наклонной пирамиды;
5. прямой пирамиды.
| |
| Какой способ надо применить при определении истинной длины рёбер прямой призмы при построении её развёртки?
| 1. способом прямоугольного треугольника;
2. способом вращения;
3. способом перемены плоскостей проекций;
4. способом плоско–параллельного перемещения;
5. никакой.
| | №
| вопрос
| варианты ответов
| |
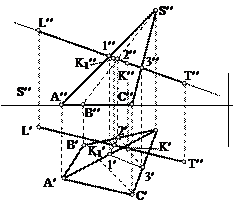
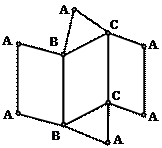
| Какой способ надо применить при определении истинной длины рёбер наклонной призмы при построении её развёртки?
| 1. способом прямоугольного треугольника;
2. способом вращения;
3. способом перемены плоскостей проекций;
4. способом плоско–параллельного перемещения;
5. никакой.
|  99 99
| Развёртка полной поверхности какого геометрического тела изображена на рисунке?
| 1. прямой призмы;
2. наклонной призмы;
3. прямого цилиндра;
4. наклонного цилиндра;
5. прямого конуса.
|  100 100
| Развёртка полной поверхности какого геометрического тела изображена на рисунке?
| 1. прямой призмы;
2. наклонной призмы;
3. прямого цилиндра;
4. наклонного цилиндра;
5. прямого конуса.
|
Заведующий каф. НГ и Г проф. Бобин Н. Е.
Составители:
проф. Онищин В. П.
доц. Эйст Ю. А.
доц. Мураев Ю. Д.
доц. Пашкевич В. М.
доц. Галушкин С. С.
асс. Игнатьев С. А.
|



 80
80
 81
81
 82
82













 86
86










 87
87
 88
88
 89
89






























 91
91
 92
92
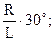 2. a =
2. a = 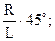 3. a =
3. a = 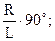 4. a =
4. a = 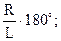 5. a =
5. a = 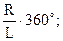 где R – радиус основания конуса?
L – длина образующих конуса.
где R – радиус основания конуса?
L – длина образующих конуса.
 99
99
 100
100