
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Г.П.Емгушева, М.Е.Чанга. ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ. Емгушева Г.П., Чанга М.Е.
Министерство образования и науки Российской Федерации
Московский государственный университет геодезии и картографии
Г.П.Емгушева, М.Е.Чанга
ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ
Учебно-методическое пособие
Москва
Издательство МИИГАиК
УДК 517.27
Е 60
Рецензенты: к.т.н., доцент Баюк О.А., к.ф.-м.н., доцент Зайцев А.А.
Емгушева Г.П., Чанга М.Е.
Исследование функций и построение графиков. Методические указания с заданиями для самостоятельного решения. – М.: Изд-во МИИГАиК, 2018. – 21с.
Содержит общий план исследования функции и краткие теоретические сведения по каждому пункту этого плана, а также примеры решения типовых задач на построение графика функции. Вторая часть пособия включает в себя 30 вариантов индивидуальных расчетных заданий для самостоятельного решения.
Предназначено для студентов 1 курса МИИГАиК, обучающихся по направлениям 21.03.03 «Геодезия и дистанционное зондирование» (бакалавр), 21.03.02 «Землеустройство и кадастры» (бакалавр), 05.03.03 «Картография и геоинформатика» (бакалавр) и другим.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
В практических задачах часто возникает необходимость детального изучения какой-либо зависимости, а также получения ее графического изображения, что позволяет наглядно представить особенности изучаемой зависимости. С математической точки зрения эта задача представляет собой исследование функции и построение ее графика. Для решения подобных задач используют методы дифференциального исчисления, причем исследование функции проводится по стандартному плану.
План исследования функции.
1. Область определения. Исследование на четность и нечетность.
2. Точки разрыва, их классификация.
3. Нули функции и промежутки знакопостоянства.
4. Экстремумы функции и промежутки монотонности.
5. Точки перегиба и промежутки выпуклости.
6. Асимптоты.
После завершения исследования на основе полученной информации строится график функции. Итак, пусть задана некоторая функция 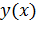 . Рассмотрим подробно каждый пункт плана исследования и прежде всего те теоретические утверждения, которые лежат в их основе.
. Рассмотрим подробно каждый пункт плана исследования и прежде всего те теоретические утверждения, которые лежат в их основе.
1. Область определения. Исследование на четность и нечетность.
Будем считать, что наша функция 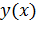 является элементарной, то есть составлена из степенной, показательной, логарифмической, тригонометрических и обратных тригонометрических функций с помощью конечного числа арифметических действий и операций композиции. В этом случае, зная области определения основных элементарных функций, легко найти область определения
является элементарной, то есть составлена из степенной, показательной, логарифмической, тригонометрических и обратных тригонометрических функций с помощью конечного числа арифметических действий и операций композиции. В этом случае, зная области определения основных элементарных функций, легко найти область определения 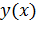 . Напомним, что, например, функция
. Напомним, что, например, функция 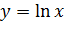 определена на промежутке
определена на промежутке 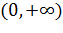 , а функция
, а функция 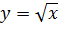 определена на промежутке
определена на промежутке 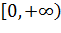 . Таким образом, выражение под знаком логарифма должно быть положительным, выражение в знаменателе не должно равняться нулю, и так далее. Из этих ограничений мы выясняем, при каких значениях переменной
. Таким образом, выражение под знаком логарифма должно быть положительным, выражение в знаменателе не должно равняться нулю, и так далее. Из этих ограничений мы выясняем, при каких значениях переменной 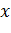 наша функция
наша функция 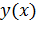 имеет смысл, то есть находим ее область определения
имеет смысл, то есть находим ее область определения 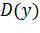 . Область определения является некоторым подмножеством числовой прямой.
. Область определения является некоторым подмножеством числовой прямой.
Если область определения симметрична относительно точки 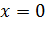 , то можно поставить вопрос о четности или нечетности нашей функции. Функция
, то можно поставить вопрос о четности или нечетности нашей функции. Функция 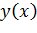 называется четной, если
называется четной, если 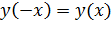 для любого
для любого 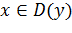 . График четной функции будет симметричным относительно оси ординат. Функция, для которой
. График четной функции будет симметричным относительно оси ординат. Функция, для которой 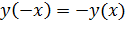 для любого
для любого 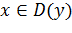 , называется нечетной, и ее график будет симметричным относительно начала координат. Если функция не будет ни четной, ни нечетной (функция общего вида), то ее график не будет иметь указанных симметрий.
, называется нечетной, и ее график будет симметричным относительно начала координат. Если функция не будет ни четной, ни нечетной (функция общего вида), то ее график не будет иметь указанных симметрий.
2. Точки разрыва, их классификация.
Функция называется непрерывной в точке a, если ее предел при x, стремящемся к a, равен ее значению в точке a.
Для поиска точек разрыва элементарных функций удобна следующая
Теорема. Любая элементарная функция непрерывна в каждой точке своей области определения.
Точку a, в которой функция 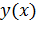 не является непрерывной, будем называть точкой разрыва функции
не является непрерывной, будем называть точкой разрыва функции 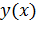 . Если в точке a существуют конечные и равные между собой пределы функции
. Если в точке a существуют конечные и равные между собой пределы функции 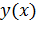 справа и слева, но они не совпадают с
справа и слева, но они не совпадают с 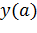 или же последнее значение не определено, то a называется точкой устранимого разрыва. Если в точке a существуют конечные, но не равные между собой пределы функции
или же последнее значение не определено, то a называется точкой устранимого разрыва. Если в точке a существуют конечные, но не равные между собой пределы функции 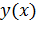 справа и слева, то a называется точкой разрыва первого рода. Наконец, если хотя бы один из односторонних пределов бесконечен или не существует, то a называется точкой разрыва второго рода.
справа и слева, то a называется точкой разрыва первого рода. Наконец, если хотя бы один из односторонних пределов бесконечен или не существует, то a называется точкой разрыва второго рода.
Таким образом, в каждой граничной точке области определения нашей функции, нужно найти ее односторонние пределы. При построении графика это поможет правильно отразить поведение функции при приближении к таким точкам.
3. Нули функции и промежутки знакопостоянства.
Точки, в которых значения нашей функции равняются нулю, называются нулями функции. Таким образом, для нахождения нулей 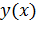 нужно решить уравнение
нужно решить уравнение 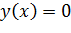 . Нули и точки разрыва функции разбивают область определения
. Нули и точки разрыва функции разбивают область определения 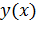 на промежутки, на каждом из которых функция сохраняет свой знак. Действительно, имеет место
на промежутки, на каждом из которых функция сохраняет свой знак. Действительно, имеет место
Теорема (Больцано-Коши). Если функция непрерывна на отрезке 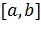 и имеет на его концах значения разных знаков, то она обращается в нуль в некоторой точке этого отрезка.
и имеет на его концах значения разных знаков, то она обращается в нуль в некоторой точке этого отрезка.
Таким образом, найдя нули функции, нужно отметить их на числовой прямой вместе с точками разрыва и выяснить знак функции на каждом из получившихся промежутков. На тех промежутках, где функция положительна, график пройдет выше оси абсцисс, а где отрицательна – ниже.
4. Экстремумы функции и промежутки монотонности.
Функция называется возрастающей (убывающей) на промежутке, если большему значению аргумента на этом промежутке соответствует большее (меньшее) значение функции.
Теорема. Если 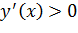 на некотором промежутке, то
на некотором промежутке, то 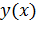 возрастает на этом промежутке. Если же
возрастает на этом промежутке. Если же 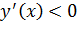 , то
, то 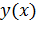 убывает.
убывает.
Точка, значение функции в которой является наибольшим (наименьшим) среди всех значений, принимаемых функцией в некоторой окрестности этой точки, называется точкой локального максимума (минимума) этой функции.
Теорема (необходимое условие экстремума). Если 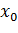 – точка локального экстремума функции
– точка локального экстремума функции 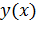 , то
, то 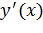 либо равна нулю в точке
либо равна нулю в точке 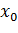 , либо не существует в этой точке.
, либо не существует в этой точке.
Точки, в которых производная функции равна нулю, либо не существует, называют критическими точками. Таким образом, все локальные экстремумы функции находятся среди ее критических точек. Каждую критическую точку следует исследовать на экстремум, пользуясь достаточными условиями экстремума.
Теорема (достаточные условия экстремума). Пусть 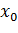 – критическая точка функции
– критическая точка функции 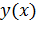 , причем
, причем 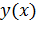 непрерывна в точке
непрерывна в точке 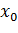 . Тогда
. Тогда
– если 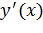 меняет знак с минуса на плюс при переходе через точку
меняет знак с минуса на плюс при переходе через точку 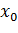 , то
, то 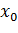 есть точка локального минимума;
есть точка локального минимума;
– если 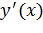 меняет знак с плюса на минус при переходе через точку
меняет знак с плюса на минус при переходе через точку 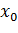 , то
, то 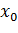 есть точка локального максимума;
есть точка локального максимума;
– если 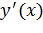 не меняет знак при переходе через точку
не меняет знак при переходе через точку 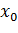 , то
, то 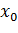 не является точкой локального экстремума.
не является точкой локального экстремума.
Таким образом, для исследования функции на монотонность и экстремумы нужно найти производную функции 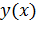 , затем приравнять ее к нулю и найти критические точки. Затем следует отметить критические точки на числовой прямой и выяснить знаки производной функции на каждом из получившихся промежутков. Промежутки, на которых производная положительна, будут промежутками возрастания функции, а промежутки, на которых производная отрицательна – промежутками убывания. С помощью достаточных условий тут же находятся точки экстремума функции.
, затем приравнять ее к нулю и найти критические точки. Затем следует отметить критические точки на числовой прямой и выяснить знаки производной функции на каждом из получившихся промежутков. Промежутки, на которых производная положительна, будут промежутками возрастания функции, а промежутки, на которых производная отрицательна – промежутками убывания. С помощью достаточных условий тут же находятся точки экстремума функции.
5. Точки перегиба и промежутки выпуклости.
Функция называется выпуклой вниз (вверх) на некотором промежутке, если ее график между любыми двумя точками этого промежутка лежит ниже (выше) хорды, стягивающей эти две точки графика. Точка непрерывности, разделяющая промежутки с разным направлением выпуклости, называется точкой перегиба.
Теорема. Если 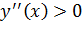 на некотором промежутке, то
на некотором промежутке, то 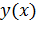 выпукла вниз на этом промежутке. Если же
выпукла вниз на этом промежутке. Если же 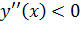 , то
, то 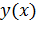 выпукла вверх.
выпукла вверх.
Таким образом, нужно найти вторую производную функции 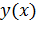 , затем те точки, в которых она обращается в нуль или не существует. Эти точки разбивают числовую прямую на промежутки и на каждом из них нужно определить знак
, затем те точки, в которых она обращается в нуль или не существует. Эти точки разбивают числовую прямую на промежутки и на каждом из них нужно определить знак 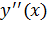 . Промежутки, на которых вторая производная положительна, будут промежутками выпуклости вниз, а промежутки, на которых вторая производная отрицательна – промежутками выпуклости вверх. После этого легко определяются точки перегиба.
. Промежутки, на которых вторая производная положительна, будут промежутками выпуклости вниз, а промежутки, на которых вторая производная отрицательна – промежутками выпуклости вверх. После этого легко определяются точки перегиба.
6. Асимптоты.
Асимптотами называются прямые, к которым неограниченно приближается график функции. Можно выделить вертикальные и наклонные асимптоты (горизонтальные асимптоты суть частный случай наклонных).
Вертикальные асимптоты описываются уравнением 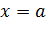 , где точка
, где точка 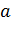 такова, что хотя бы один из односторонних пределов функции
такова, что хотя бы один из односторонних пределов функции 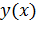 в этой точке бесконечен. Для нахождения вертикальных асимптот нужно проанализировать результаты пункта 2, где вычислялись односторонние пределы в граничных точках области определения.
в этой точке бесконечен. Для нахождения вертикальных асимптот нужно проанализировать результаты пункта 2, где вычислялись односторонние пределы в граничных точках области определения.
Наклонные асимптоты описываются уравнением 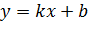 , при этом случаю
, при этом случаю 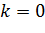 отвечают горизонтальные асимптоты. При этом функция может иметь до двух наклонных асимптот (при
отвечают горизонтальные асимптоты. При этом функция может иметь до двух наклонных асимптот (при 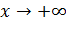 и при
и при 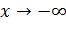 ). Параметры
). Параметры 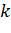 и
и 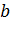 вычисляются по формулам
вычисляются по формулам
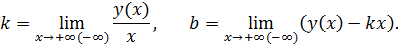
Нужно иметь в виду, что асимптота существует лишь в том случае, если оба указанных предела существуют и конечны.
Построение графика функции
При построении графика рекомендуется сначала пунктиром нанести на координатную плоскость асимптоты, чтобы впоследствии было удобно и наглядно «вписывать» в них будущий график. Затем нанести характерные точки графика: нули функции, точки экстремума и точки перегиба. Наконец, пользуясь информацией о знаке функции, характере ее монотонности и выпуклости, нарисовать график. В случае четной (нечетной) функции достаточно построить график для положительных значений 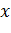 и пользоваться соответствующей симметрией.
и пользоваться соответствующей симметрией.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Пример 1. Построить график функции 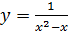 , применяя общую схему исследования функции при помощи производных.
, применяя общую схему исследования функции при помощи производных.
Решение.
1)Найдемобласть определения функции. Функция 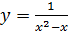 определена при всех значениях
определена при всех значениях 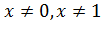 , то есть
, то есть 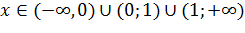 . Исследуем функцию на четность, нечетность. Функция
. Исследуем функцию на четность, нечетность. Функция 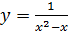 общего вида, так как ее область определения не симметрична относительно точки
общего вида, так как ее область определения не симметрична относительно точки 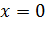 .
.
2)Точками разрыва функции являются точки 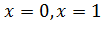 , так как в этих точках функция не определена (см.п.1)). Рассмотрим односторонние пределы функции в этих точках:
, так как в этих точках функция не определена (см.п.1)). Рассмотрим односторонние пределы функции в этих точках: 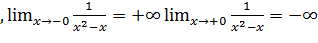 , следовательно, точка
, следовательно, точка 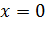 является точкой разрыва второго рода. Аналогично,
является точкой разрыва второго рода. Аналогично, 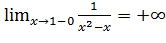 ,
, 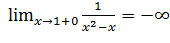 , значит, точка
, значит, точка 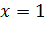 также является точкой разрыва второго рода.
также является точкой разрыва второго рода.
3) Найдем нули функции, то есть решим уравнение 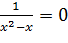 , решений нет. Значит, график функции не пересекает ось
, решений нет. Значит, график функции не пересекает ось 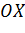 и ось
и ось 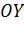 . Промежутки знакопостоянства определяются из неравенства
. Промежутки знакопостоянства определяются из неравенства 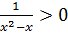 , откуда
, откуда
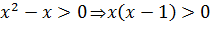 . Решим неравенство методом интервалов:
. Решим неравенство методом интервалов:

Из рисунка видно, что 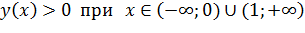 ,
,
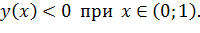
4) Для нахождения экстремума функции найдем критические точки, то есть вычислим производную функции и приравняем ее к нулю.

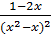
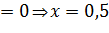 критическая точка.
критическая точка.
Используя достаточные условия монотонности функции найдем промежутки возрастания и убывания функции для этого воспользуемся методом интервалов.


| X |
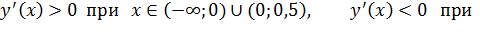
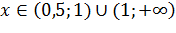 , то функция
, то функция 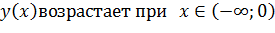 и при
и при 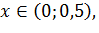 убывает
убывает 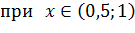 и при
и при 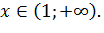 Следовательно, точка
Следовательно, точка 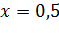 является точкой максимума, так как
является точкой максимума, так как 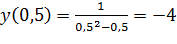 , то точка
, то точка 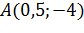 максимум функции.
максимум функции.
5) Найдем точки перегиба и промежутки выпуклости функции с помощью второй производной.
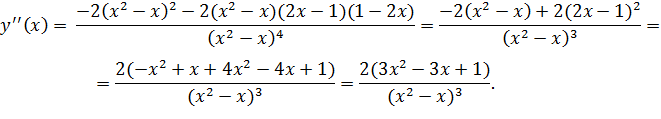
Вторая производная 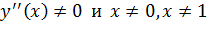 , следовательно, точек перегиба нет.
, следовательно, точек перегиба нет.
Для нахождения промежутков выпуклости функции решим неравенство
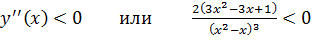 , так как
, так как 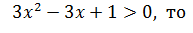 решим неравенство
решим неравенство 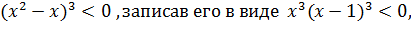 применим метод интервалов ( см.п.3)), тогда
применим метод интервалов ( см.п.3)), тогда 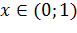 и
и 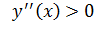 при
при 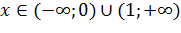 . Таким образом, функция выпукла вверх (выпукла) при
. Таким образом, функция выпукла вверх (выпукла) при 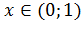 и функция выпукла вниз (вогнута) при
и функция выпукла вниз (вогнута) при 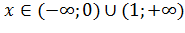 .
.
6) Асимптоты. Так как точками разрыва функции являются точки 
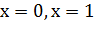 и
и 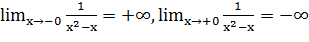 ,
, 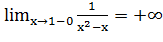 ,
, 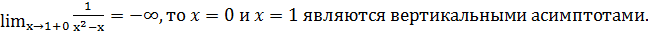
Найдем наклонные асимптоты в виде 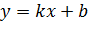 . Вычислим параметры
. Вычислим параметры 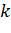 и
и 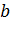 по формулам
по формулам 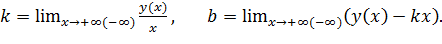
Имеем 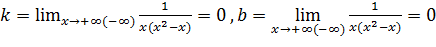 . Тогда
. Тогда 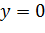
горизонтальная асимптота.
7)Построение графика функции.
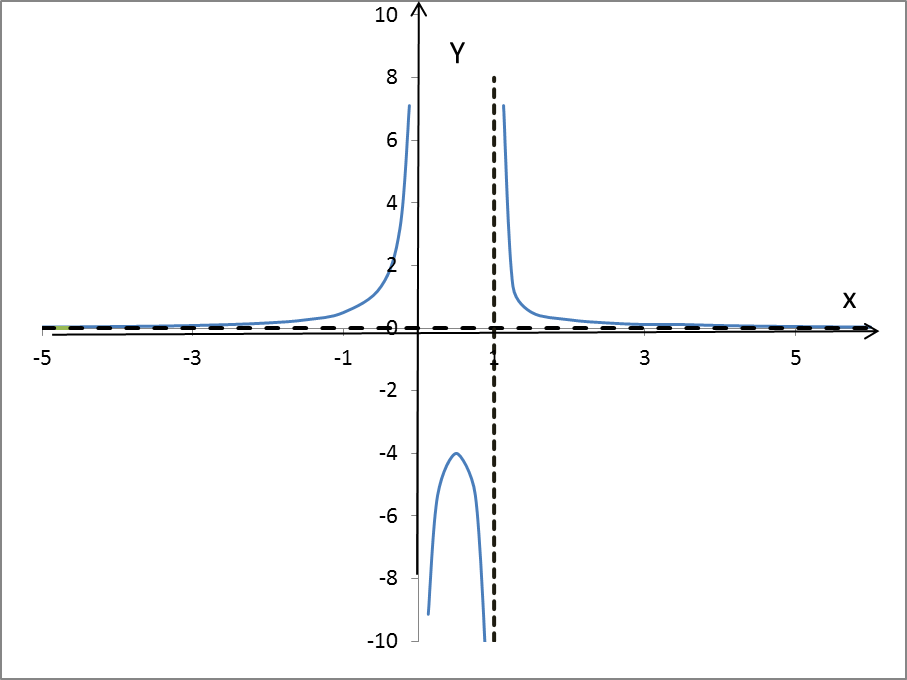
Пример 2. Исследовать функцию 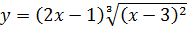 и построить ее график
и построить ее график 
Решение.
1) Найдемобласть определения функции. Функция
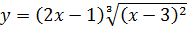 определена при всех значениях
определена при всех значениях 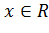 , то есть
, то есть 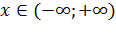 . Исследуем функцию на четность, нечетность. Так как
. Исследуем функцию на четность, нечетность. Так как 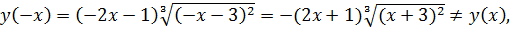 следовательно, функция
следовательно, функция 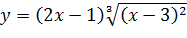 общего вида.
общего вида.
2) Точек разрыва у функции нет.
3) Найдем нули функции: решим уравнение 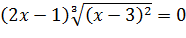 , откуда
, откуда 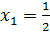 ,
, 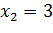 . Значит, график функции пересекает ось
. Значит, график функции пересекает ось 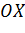 в точках
в точках 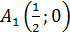 ,
, 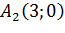 . Промежутки знакопостоянства определим из неравенства
. Промежутки знакопостоянства определим из неравенства
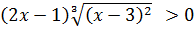 , откуда
, откуда 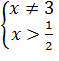 .
.
Таким образом, 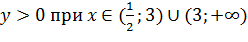 и
и 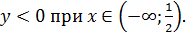
Найдем точки пересечения функции с осью OY : 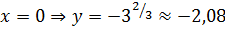 . Отсюда имеем точку
. Отсюда имеем точку 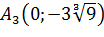 .
.
4) Для нахождения экстремума функции найдем критические точки. Вычислим производную
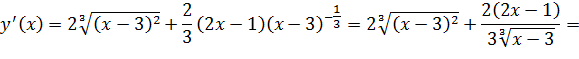
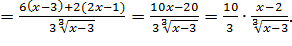
Найдем критические точки функции, то есть решим уравнение 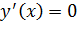 или точки, в которых
или точки, в которых 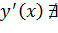 . Получим
. Получим
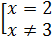 . Точки
. Точки 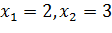 являются критическими.
являются критическими.
Используя достаточные условия монотонности функции найдем промежутки возрастания и убывания функции для этого воспользуемся методом интервалов.
| y'(x): + - + y(x): |
| 3 X |
 Так как
Так как 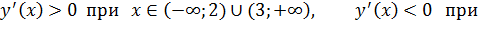
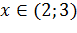 , то функция
, то функция 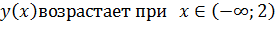
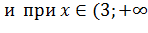 ), убывает при
), убывает при 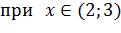 , Следовательно, точка
, Следовательно, точка 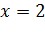 является точкой максимума, а точка
является точкой максимума, а точка 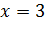 – точка минимума, так как
– точка минимума, так как 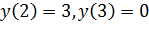 , то точка
, то точка 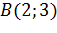 максимум функции, а точка
максимум функции, а точка 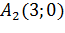 минимум функции, то есть точки
минимум функции, то есть точки 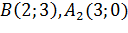 экстремумы функции.
экстремумы функции.
5) Найдем точки перегиба и промежутки выпуклости функции с помощью второй производной.
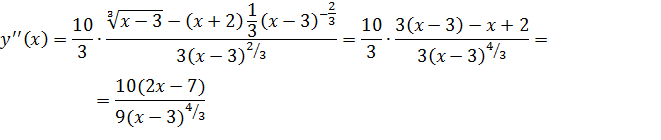
Так как 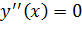 при
при 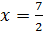 , то исследуем поведение второй производной слева и справа от точки
, то исследуем поведение второй производной слева и справа от точки 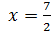 :
:
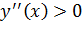 при
при 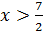 и
и 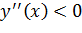 при
при 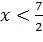 , следовательно, функция выпукла вниз (вогнута) при
, следовательно, функция выпукла вниз (вогнута) при 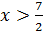 и функция выпукла вверх (выпукла)
и функция выпукла вверх (выпукла) 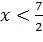 . Таким образом, точка
. Таким образом, точка 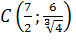 является точкой перегиба.
является точкой перегиба.
6) Асимптоты. Вертикальных асимптот нет, так как функция непрерывна на всей числовой прямой. Найдем наклонные асимптоты в виде 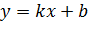 . Вычислим параметр
. Вычислим параметр 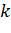 по формуле
по формуле 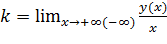 .
.
Имеем 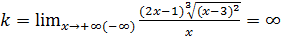 . Следовательно, наклонных асимптот нет.
. Следовательно, наклонных асимптот нет.
7)Построение графика функции.
|
|
|
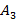
|
| X |
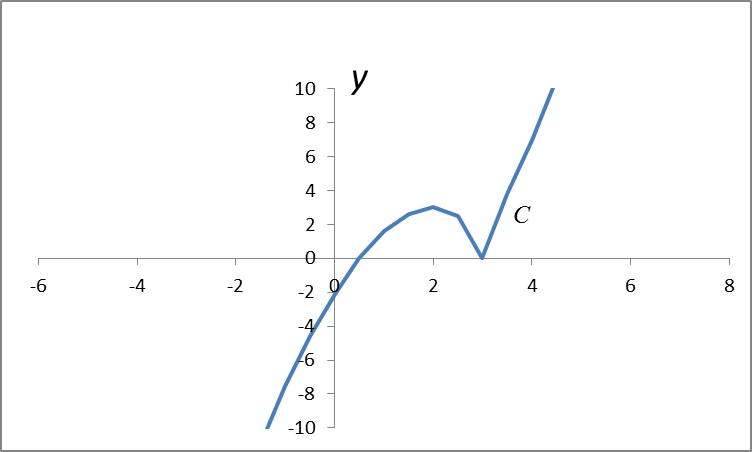
Пример 3. Исследовать функцию 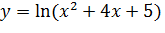 и построить ее график
и построить ее график 
Решение.
1) Найдемобласть определения функции. Функция 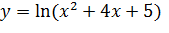 определена при
определена при 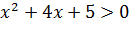 , так как это неравенство справедливо при всех значениях
, так как это неравенство справедливо при всех значениях 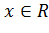 , то
, то 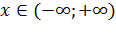 .
.
Исследуем функцию на четность, нечетность. Так как
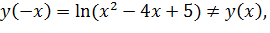 следовательно, функция
следовательно, функция 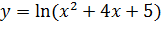 общего вида.
общего вида.
2) Точек разрыва у функции нет.
3) Найдем нули функции: решим уравнение 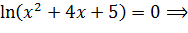
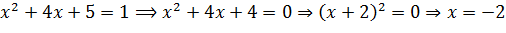 . Значит, график функции пересекает ось
. Значит, график функции пересекает ось 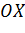 в точке
в точке 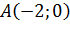 . Промежутки знакопостоянства определим из неравенства
. Промежутки знакопостоянства определим из неравенства 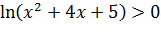 откуда
откуда 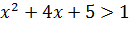 или
или 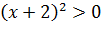 , откуда
, откуда 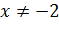 . Значит,
. Значит, 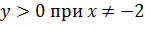 .
.
Найдем точки пересечения функции с осью OY: 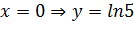 , то есть точкой пересечения с осью OY является точка
, то есть точкой пересечения с осью OY является точка 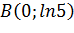 .
.
4) Для нахождения экстремума функции найдем критические точки. Вычислим производную и приравняем ее к нулю:
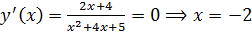 является критической точкой.
является критической точкой.
Используя достаточные условия монотонности функции найдем промежутки возрастания и убывания функции.
Так как 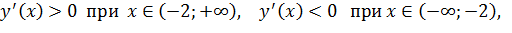 то функция
то функция 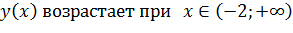 и убывает при
и убывает при
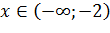 . Следовательно, точка
. Следовательно, точка 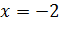 является точкой минимума, так как
является точкой минимума, так как 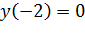 , то точка
, то точка 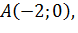 является, одновременно, нулем и минимумом функции.
является, одновременно, нулем и минимумом функции.
5) Найдем точки перегиба и промежутки выпуклости функции с помощью второй производной.
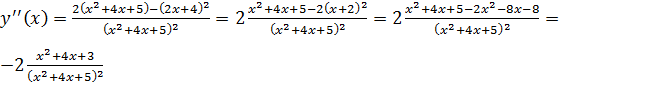 .
.
Решим уравнение 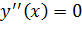 , откуда
, откуда 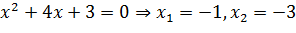 .
.
Чтобы определить выпуклость и вогнутость функции, решим неравенство 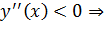
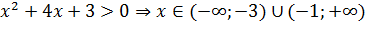 .
.
Значит, функция выпукла вверх (выпукла) при 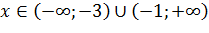 и функция выпукла вниз (вогнута) при
и функция выпукла вниз (вогнута) при 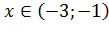 . Найдем
. Найдем 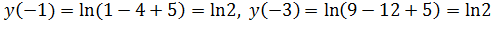 . Таким образом, точки
. Таким образом, точки 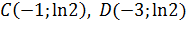 являются точками перегиба.
являются точками перегиба.
6) Асимптоты. Вертикальных асимптот нет, так как функция непрерывна на всей числовой прямой. Найдем наклонные асимптоты в виде 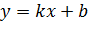 . Вычислим параметры
. Вычислим параметры 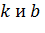 по формулам:
по формулам: 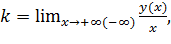
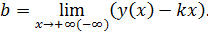
Имеем 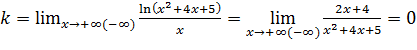 ,
,
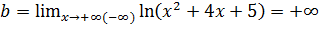 . Следовательно, наклонных асимптот нет.
. Следовательно, наклонных асимптот нет.
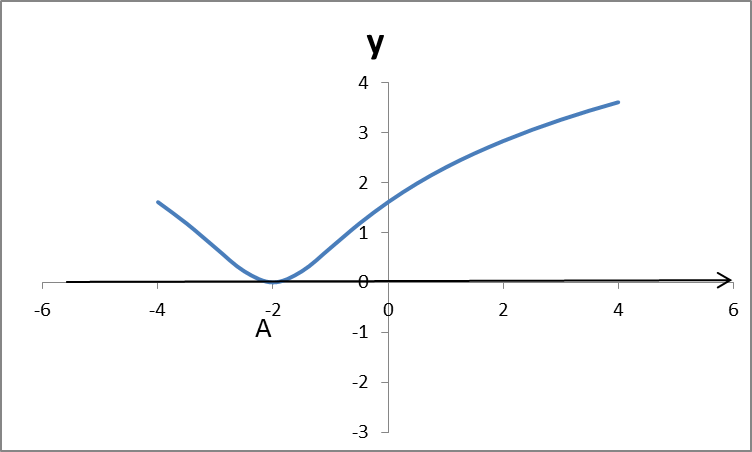
7)Построение графика функции.
| X |
| B |
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Провести полное исследование функции и построить ее график.
Вариант 1. 1. 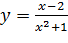 ; 2.
; 2. 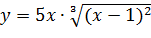 .
.
Вариант 2. 1. 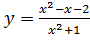 ; 2.
; 2. 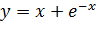 .
.
Вариант 3. 1. 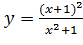 ; 2.
; 2. 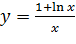 .
.
Вариант 4. 1. 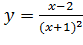 ; 2.
; 2. 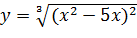 .
.
Вариант 5. 1. 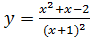 ; 2.
; 2. 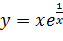 .
.
Вариант 6. 1. 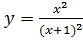 ; 2.
; 2. 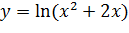 .
.
Вариант 7. 1. 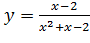 ; 2.
; 2. 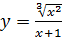 .
.
Вариант 8. 1. 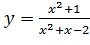 ; 2.
; 2. 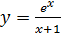 .
.
Вариант 9. 1. 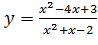 ; 2.
; 2. 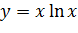 .
.
Вариант 10. 1. 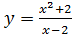 ; 2.
; 2. 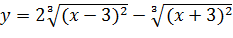 .
.
Вариант 11. 1. 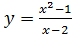 ; 2.
; 2. 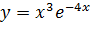 .
.
Вариант 12. 1. 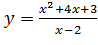 ; 2.
; 2. 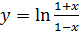 .
.
Вариант 13. 1. 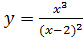 ; 2.
; 2. 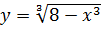 .
.
Вариант 14. 1. 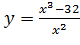 ; 2.
; 2. 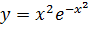 .
.
Вариант 15. 1. 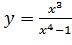 ; 2.
; 2. 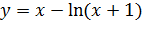 .
.
Вариант 16. 1. 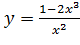 ; 2.
; 2. 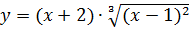 .
.
Вариант 17. 1. 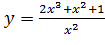 ; 2.
; 2. 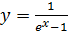 .
.
Вариант 18. 1. 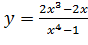 ; 2.
; 2. 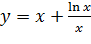 .
.
Вариант 19. 1. 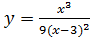 ; 2.
; 2. 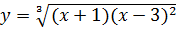 .
.
Вариант 20. 1. 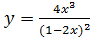 ; 2.
; 2. 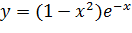 .
.
Вариант 21. 1. 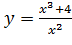 ; 2.
; 2. 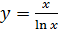 .
.
Вариант 22. 1. 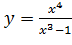 ; 2.
; 2. 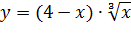 .
.
Вариант 23. 1. 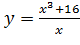 ; 2.
; 2. 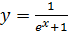 .
.
Вариант 24. 1. 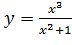 ; 2.
; 2. 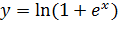 .
.
Вариант 25. 1. 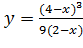 ; 2.
; 2. 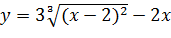 .
.
Вариант 26. 1. 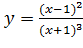 ; 2.
; 2. 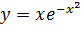 .
.
Вариант 27. 1. 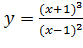 ; 2.
; 2. 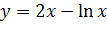 .
.
Вариант 28. 1. 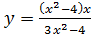 ; 2.
; 2. 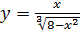 .
.
Вариант 29. 1. 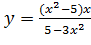 ; 2.
; 2. 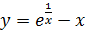 .
.
Вариант 30. 1. 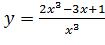 ; 2.
; 2. 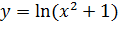 .
.
ЛИТЕРАТУРА
1. Кудрявцев Л.Д. Математический анализ. В 2-х т. М.: Высшая школа, 1970.
2. Шипачев В.С. Высшая математика. М.: Высшая школа, 1998.
3. Берман Г.Н. Сборник задач по курсу математического анализа. М.: Наука, 1985.
4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. М.: Высшая школа, 1986.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|