
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Математический анализ. Вопрос №9
Математический анализ. Вопрос №9
Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Рассмотреть определенный интеграл с переменным верхним пределом интегрирования. Доказать, что если подынтегральная функция непрерывна, то производная по верхнему пределу равна подынтегральной функции. Вывести формулу Ньютона-Лейбница. Показать на примере применение этой формулы.
Ответ.
Рассмотрим функцию y=f(x), интегрируемую на отрезке [a, b]. Если x на промежутке [a, b], то функция f(x) интегрируема на любом отрезке [a, x]. Предположим, что x меняется на отрезке [a, b], то на этом отрезке определена функция
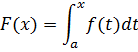
Формула 1.
(Переменную интегрирования обозначим буквой t, переменный верхний предел – буквой x).
Теорема. Если подынтегральная функция непрерывна, то производная определенного интеграла с переменным верхним пределом существует и равна значению подынтегральной функции для этого предела, т.е. (Написал без доказательства, там темный лес.)
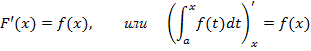
Формула 2
Формула Ньютона-Лейбница. Известно, что любые две первообразные функции f отличатся друг от друга только на константу (число). Интеграл 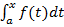 является одной из первообразных функции f; тогда произвольную первообразную этой функции можно найти по формуле:
является одной из первообразных функции f; тогда произвольную первообразную этой функции можно найти по формуле:
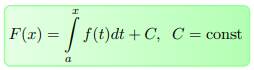
Формула 3
Вычислим значения первообразной F(x) в точках x = a и x = b:
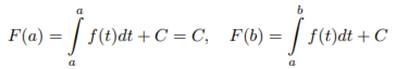
Формула 4
Мы воспользовались тем, что, согласно свойствам определенного интеграла, 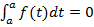 . Из формулы 4 следует формула Ньютона – Лейбница:
. Из формулы 4 следует формула Ньютона – Лейбница:
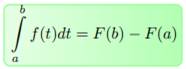
Формула 5
Формула Ньютона-Лейбница говорит о том, что для вычисления определенного интеграла функции f нужно составить разность значений любой из ее первообразных на вернем и нижнем пределах интеграла. Формулу 5 часто записывают в более короткой форме:
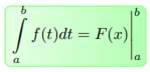
Формула 6
Пример (на применение формулы Н – Л).
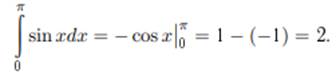
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|