
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
МЕТОД ЭКВИВАЛЕНТНЫХ ПРЕОБРАЗОВАНИЙ
МЕТОД ЭКВИВАЛЕНТНЫХ ПРЕОБРАЗОВАНИЙ
Используется для расчета цепей, если цепь простая, содержит, как в данном случае один источник ЭДС. При этом участки цепи, характеризующиеся своими сопротивлениями, могут быть преобразованы с использованием правил последовательно-параллельных преобразований (см. Материалы для самостоятельной проработки 1). Задача ставится так:
Значение ЭДС известно, параметры ветвей известны. Необходимо найти токи во всех ветвях цепи.
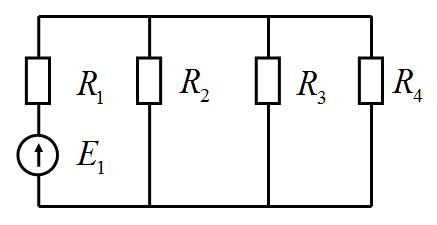
Рис. 1
РЕШЕНИЕ: Произвольно выберем направления вычислений токов в ветвях. Например, так.
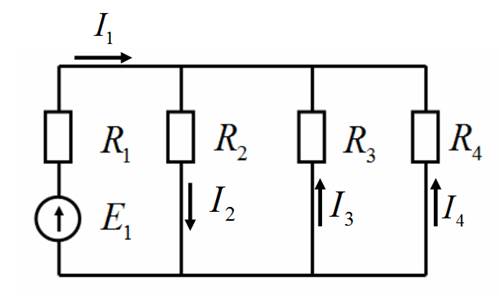
Рис.2
Эти токи и будем искать.
Для этого определимся, какие участки соединены последовательно, а какие параллельно. Внимание! Преобразования всегда осуществляются с участка цепи противоположного источнику.
Измерения показали, что сопротивлениясоединены параллельно по отношению друг к другу, так как при одинаковом напряжении и разных сопротивлениях токи разные (см. свои вычисления в протоколе). Следовательно, этот участок цепи можно заменить одним сопротивлением (эквивалентным). Помним, что при параллельном соединении эквивалентная проводимость равна сумме проводимостей всех ветвей.
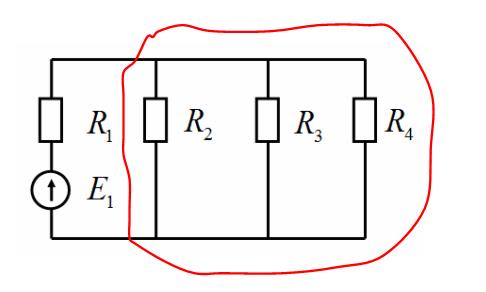
Рис.3
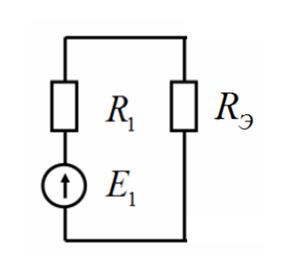 а
а
|
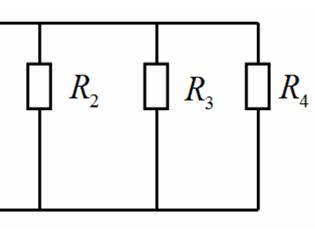 б
б
|
Рис.4
Следовательно, эквивалентное сопротивление для рис. 4,б можно определить, используя выражение
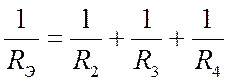
Внимание! Это еще не эквивалентное сопротивление. Его, 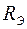 , еще нужно выразить. По желанию привести к общему знаменателю справа и т. д. Однако, удобно сначала подставить численные значения вместо
, еще нужно выразить. По желанию привести к общему знаменателю справа и т. д. Однако, удобно сначала подставить численные значения вместо 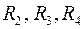 ,найти сумму. После чего взять обратную величину (см. пример с численными значениями). То есть
,найти сумму. После чего взять обратную величину (см. пример с численными значениями). То есть
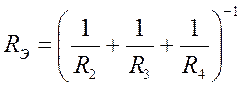 .
.
При этом нужно понимать, что при делении результат тем точнее, чем больше значащих цифр остается. В вашей работе минимум 4-5.
В результате преобразований можно легко найти ток в ветви с источником, используя второй закон Кирхгофа. При этом стрелка тока 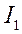 соответствует указанной на рис. 2.
соответствует указанной на рис. 2.
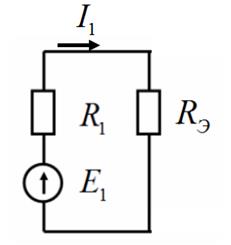
Рис.5
ПРОИЗВОЛЬНО выберем направление обхода контура и в соответствии со 2 законом Кирхгофа получим 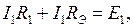 или
или 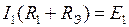 .
.
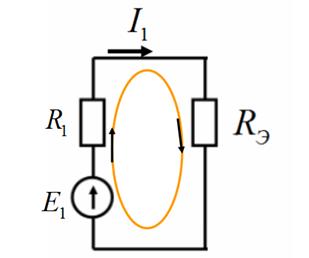
Рис.6
В этом уравнении неизвестным является ток 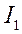 . Остальные параметры заданы по условию. Тогда
. Остальные параметры заданы по условию. Тогда
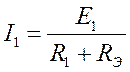 .
.
_____________________________
Определим токи 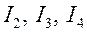 . Для этого свернутую схему рис. 4,а разворачиваем (рис.7). Поскольку ток
. Для этого свернутую схему рис. 4,а разворачиваем (рис.7). Поскольку ток 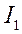 уже известен, то для первого контура (желтого) произвольно выберем направление обхода и воспользуемся вторым законом Кирхгофа. Тогда уравнение будет иметь вид
уже известен, то для первого контура (желтого) произвольно выберем направление обхода и воспользуемся вторым законом Кирхгофа. Тогда уравнение будет иметь вид
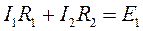 ,
,
откуда найдем ток 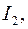 так как все остальное известно, т.е.
так как все остальное известно, т.е.
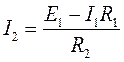 .
.
____________________________________________________
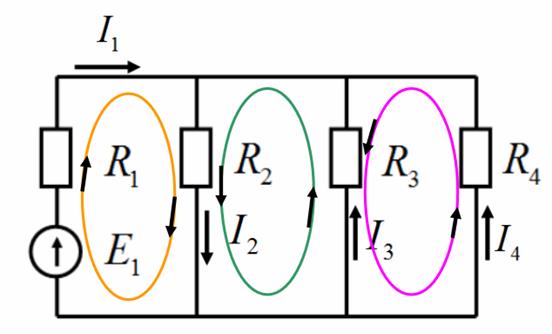
Рис.7
Аналогично в соответствии с выбранным обходом получаем для зеленого контура
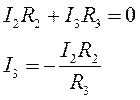 ,
,
для розового контура имеем
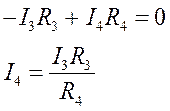
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|