Графический способ определения главных напряжений и положения главных площадок при плоском напряженном состоянии (круги Мора).

35. Графический способ определения главных напряжений и положения главных площадок при плоском напряженном состоянии (круги Мора).

Если в формулах для определения напряжений на произвольной площадке при плоском напряжённом состоянии исключить α, то получим зависимость τ _α = f (σ_α), которая в осях σ, τ отображает окружность с центром на оси σ. О.Х. Мор использовал это обстоятельство для определения напряжений графическим способом. При этом можно решить вида задач.

I задача (прямая).

Дано: σ_I, σ_II, α (рис. 4.10).

Требуется определить: σ_α , τ_α .

Изложим последовательность операций, а затем докажем, что они правомерны.

Проведём оси σ, τ (рис. 4.11) и отложим отрезки, равные главным напряжениям ОА = σ_I , ОВ = σ_II. На отрезке ВА, как на диаметре, построим окружность с центром в точке С. Полученная окружность, называется кругом Мора или кругом напряжений. Проведём из центра окружности С радиус под углом 2 α от оси σ против хода часовой стрелки (так как считаем, что угол α положительный) и докажем, что координаты полученной точки D_α соответствуют напряжениям на площадке α, то есть ОК_α= σ_α.

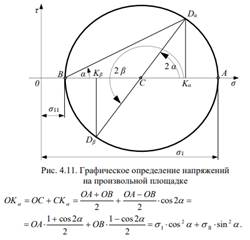
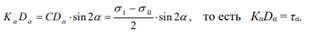
Итак, мы доказали, что с помощью круга Мора, можно определить напряжения на произвольной площадке α. Следовательно, задача решена.

Важный вывод: точки, соответствующие двум взаимно перпендикулярным площадкам, лежат на концах одного диаметра круга Мора.

II задача (обратная).

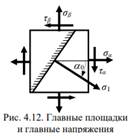
Дано: σ α , τ α , σ β , τ β (рис. 4.12). Требуется определить: σI , σI I , α0 .

Эта задача имеет для практики более важное значение, чем прямая задача.

Проводим координатные оси (рис. 4.13) σ, τ и строим в этих осях точки D_α (σ_α , τ_α ), D_β (σ_β , τ_β ). Так как эти точки соответствуют взаимно перпендикулярным площадкам, то они лежат на концах одного диаметра круга Мора. Соединяем эти точки и определяем положение центра круга С. Имея центр и диаметр, можно провести единственную окружность. Задача решена.

ОА = σ_I, ОВ = σ_II.

Проведём хорду BD_α и получим угол α от σ_I до σ_α , а нам нужен угол α₀ от σ₀ до σ_I. Следовательно, α₀ = – α.

Проводим хорду BD'α, где D'_α зеркальное отображение точки D_α .относительно горизонтальной оси. Угол ABD'α и есть искомый угол α₀.

Используя круг Мора, выведем аналитические зависимости для определения главных напряжений: