
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Численные методы. Тема: Решение задач численными методами.. Теоретическая часть.
Министерство образования и науки Красноярского края
КГБПОУ «Боготольский техникум транспорта»
Занятие по теме:
Численные методы
Методические указания для специальности
23.02.06 Техническая эксплуатация подвижного состава железных дорог
среднего профессионального образования базовой подготовки
Уважаемые студенты, вашему вниманию предложен теоретический и практический материал по теме «Численные методы». Необходимо его изучить и выполнить задачи Практической части. Всего пять вариантов. Распределение вариантов по списку, например:
Номер по списку – вариант
1 – 1
2 – 2
3 – 3
4 – 4
5 – 5
6 – 1
7 – 2
8 – 3
9 – 4
10 – 5 и т.д.
Выполнить задания в электронном виде с помощью текстового редактора Word или рукописно в тетради в клеточку и фотоотчёт прислать преподавателю. Возможно, сдать работы лично преподавателю.
С уважением Светлана Яковлевна Щуревич!
Контакты:
Соцсети (рекомендую): https://vk.com/the_sand23
e-mail: Svetlana_17.12@mail.ru
Тема: Решение задач численными методами.
Цели:
 Изучить вычисление определенных интегралов численными методами.
Изучить вычисление определенных интегралов численными методами.
 Развивать логическое мышление, память, внимание и самостоятельность.
Развивать логическое мышление, память, внимание и самостоятельность.
Литература: Лисичкин В.Т., Соловейчик И.Л. Математика: Учеб. Пособие для техникумов. – М.: Высш. шк., 1991. – 480 с.: ил.
Теоретическая часть.
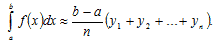
 Значения у0, у1,..., уn находят из равенств
Значения у0, у1,..., уn находят из равенств 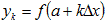 , к = 0, 1..., n .Эти формулы называются формулами прямоугольников и дают приближённый результат. С увеличением n результат становится более точным.
, к = 0, 1..., n .Эти формулы называются формулами прямоугольников и дают приближённый результат. С увеличением n результат становится более точным.
Итак, чтобы найти приближённое значение интеграла нужно:
- разделить отрезок интегрирования [a, b] на n равных частей точками х0= а, х1, х2,..., х n -1, х n = b ;
- вычислить значения подынтегральной функции
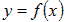 в точках деления, т.е. найти у 0 = f (x0), у 1 = f (x1), у 2 = f (x2), у n -1 = f (xn-1), у n = f (xn) ;
в точках деления, т.е. найти у 0 = f (x0), у 1 = f (x1), у 2 = f (x2), у n -1 = f (xn-1), у n = f (xn) ; - воспользоваться одной из приближённых формул.
Для того, чтобы найти погрешность вычислений, надо воспользоваться формулами:
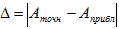
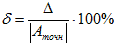
| Алгоритм применения метода прямоугольников для нахождения приближённого значения интеграла | Пример применения метода прямоугольников. |

| 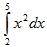
|
| 1.Разобьём отрезок [a,b] на n равных частей. | 1. Пусть n=6. |
2.  Найдем Найдем
| 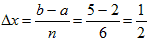 2. 2.
|
3. Найдем точки деления:
х k = a + k  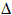 х
k=0,1,…,n х
k=0,1,…,n
| 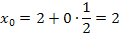 3. 3.
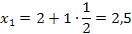
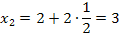 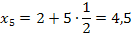
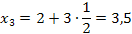 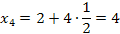
|
| 4. Найдем значение функции в точках деления: у 0 = f(x0), у 1 = f(x1), у 2 = f(x2), у n -1 = f (xn-1), у n = f (xn); | 4.
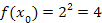
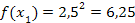
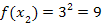
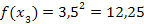
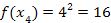
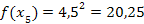
|
5. Подставим полученные значения в формулу:
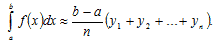
| 5.
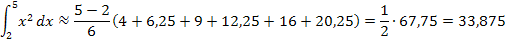
|
| 6. Вычислим точное значение интеграла. | 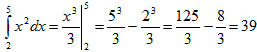 6.
6.
|
7. Вычислим погрешность:
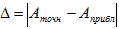
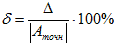
| 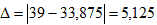
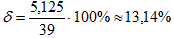 7. 7.
|
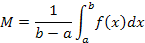 Практическая часть.
Практическая часть.
1.Найти среднее значение M функции f(x), используя формулу
если данная функция непрерывна, а аргумент x изменяется от a до b.
1.1

1.2
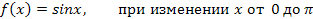
1.3
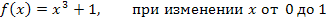
1.4
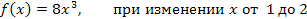
1.5
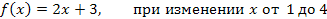
2.Изучить метод трапеций (стр. 350, п.4) и составить таблицу, используя №352:

| Алгоритм применения метода трапеций для нахождения приближённого значения интеграла | Пример применения метода трапеций. |

| 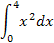
|
3.Вычислить интегралы методом прямоугольников и методом трапеций. Сравнить полученные результаты. Найти относительную погрешность вычислений.
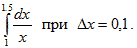 3.1 3.1
| 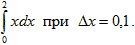 3.3 3.3
|  3.5 3.5
|
 3.2 3.2
| 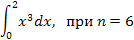 3.4 3.4
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|