- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
МЕТОДИЧЕСКИЕ УКАЗАНИЯ. к практическим занятиям. по дисциплине. Основы организации и управления в строительстве». Ставрополь, 2018. Содержание
Министерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное учреждение
профессионального образования
«Северо-Кавказский федеральный университет»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям
по дисциплине
«Основы организации и управления в строительстве»
для бакалавров направления 08.03.01
«Строительство»
ЧАСТЬ 1
Ставрополь, 2018
Методические указания составлены в соответствии с требованиями ФГОС ПО по специальности 08.03.01 «Промышленное и гражданское строительство» и программы дисциплины «Основы организации и управления в строительстве».
В методических указаниях к практическим занятиям рассматриваются следующие вопросы: основы поточного метода строительства, сетевое моделирование строительного производства, календарное планирование производства строительно-монтажных работ, проектирование стройгенплана и его элементов .
Методические указания могут быть использованы для самостоятельной работы студентов.
Составитель: Е.Н.Белая, ст.преп.
Рецензент: А.Т. Максименко, канд. арх., доцент
Содержание
Введение. 4
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1 Построение сетевого графика. Правила построения. Элементы сетевой модели. 5
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 2 Расчет параметров сетевой модели табличным (аналитическим) способом.. 12
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3 Расчет параметров сетевого графика непосредственно на его поле в секторной форме 20
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 4 Расчет параметров сетевого графика непосредственно на его поле в форме дроби. 25
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 5 Расчет параметров сетевого графика с определением потенциалов событий. 29
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 6 Построение и расчет сетевых графиков в терминах работ. 31
Введение
Изучению дисциплины «Основы организации и управления в строительстве» предшествует изучение таких специальных дисциплин, как «Технология строительного производства» и «Технология строительных процессов».
При подготовке к каждому занятию необходимо проработать ту тему лекционного курса, на основе которой проводится практическое занятие. Ознакомиться с краткими пояснениями основных положений по расчёту, который приводится в теоретической части, разобрать пример решения задачи, приводимый к практическому занятию.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1
Построение сетевого графика. Правила построения. Элементы сетевой модели.
Теоретическая часть
Сетевая модель представляет собой ориентированный граф, отражающий последовательность и организационно-технологические взаимосвязи между работами, выполнение которых требуется для достижения поставленной цели. Сетевая модель, представленная графически на плоскости с рассчитанными временными и ресурсными параметрами, называется сетевым графиком.
На сетевых графиках, представляющих собой стрелочную диаграмму, схематически отображается последовательность выполнения работ и их взаимосвязи в процессе производства. Основными элементами сетевых графиков являются:
Работы — это производственный процесс, который необходимо выполнить для получения законченного промежуточного результата (изображаются сплошной стрелкой);
События — результат завершения одной или нескольких работ, дающий возможность начать последующие по технологии строительства работы (изображаются кружком с порядковым номером события);
Ожидания — это, по сути, работа, но только требующая затрат времени и не требующая затрат ресурсов (изображаются сплошной стрелкой с указанием причины);
Зависимости – фиктивные работы, которые не открывают непосредственно возможность выполнения последующих работ, но они должна быть выполнены к их началу (пунктирная стрелка);
Путь – это непрерывная последовательность работ от исходного до завершающего события сетевого графика. Путь на сетевом графике от исходного события до завершающего, имеющий наибольшую продолжительность по времени, называется критическим путем.
Сетевой график должен отражать организационно-технологическую модель возведения зданий и сооружений и удовлетворять требованиям технологии строительного производства. При построении сетевого графика необходимо руководствоваться следующими правилами:
- все стрелки-работы, стрелки-ожидания и стрелки-зависимости должны быть направлены в одну сторону развития работ от исходного события к завершающему;
- все события должны быть пронумерованы, при этом каждое последующее событие должно иметь больший номер, чем событие, ему предшествующее;
- не допускается повторение номеров событий;
- при обозначении двух и более параллельно выполняемых работ необходимо введение дополнительных событий и зависимостей, т.к. в противном случае разные строительные процессы будут иметь одинаковый шифры (см. рис. 1)
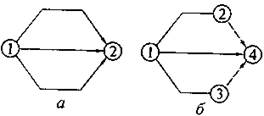 |
Рисунок 1 - Изображение на сетевом графике параллельного выполнения работ:
а — неправильно; б — правильно
- все события, кроме завершающего, должны иметь последующие работы. В тех случаях, когда завершение работы не обусловливает начало каких-либо работ, его относят к конечному событию;
- в сетевом графике не должно быть замкнутых контуров (рис. 2, а), «хвостов» (рис. 2, б), тупиковых работ (рис. 2, в) и пересечений работ (зависимостей).
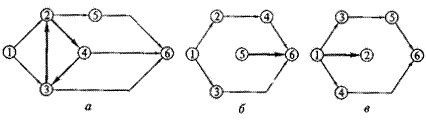 |
Рисунок 2 - Недопустимые изображения на сетевых графиках (выделены жирными стрелками): а — замкнутый контур; б — «хвост»; в — тупик
Если последующие работы можно начать после выполнения предшествующей работы не полностью, а частично, то она разделится на соответствующие части со своими событиями их завершения (т.е. расчленяется на несколько работ), и увязка выполнения последующих работ производится с указанными событиями (рис. 3).
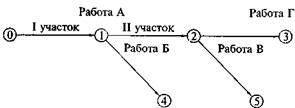
Рисунок 3 - Изображение на сетевых графиках разделения работ на части (участки)
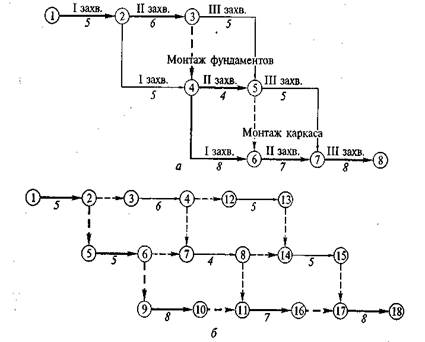
Если на объекте организуется поточный процесс производства работ, то на сетевом графике он должен отображаться согласно рис. 4 в соответствии с принятой разбивкой фронта работ на захватки. Если на объекте организуется поточный процесс производства работ, то на сетевой модели он отражается в соответствии с принятой разбивкой фронта работ на захватки (ярусы). При этом на каждой горизонтальной линии могут описываться либо все строительные процессы, происходящие на одной захватке(«горизонталь-захватка»),либо отдельный технологический процесс, выполняемый на всех захватках данного объекта(«горизонталь-процесс»). Если сетевая модель разрабатывается по схеме «горизонталь-захватка», она развивается преимущественно в горизонтальном направлении, что удобно с позиции графической компоновки чертежа. Для многоэтажных зданий, предусматривающих деление фронта работ на многочисленные ярусы, можно рекомендовать схему «горизонталь-процесс». Рассмотрим обе схемы. На рисунке 4 представлена схема «горизонталь-захватка», на рисунке 5 - «горизонталь-процесс»
Как видно из рис. 4, а, если не вводить дополнительные события, то при расчете графика критический путь (1—2, 2—3, 3—4, 4—5, 6—7, 7—8), выделенный на графике жирной ломаной линией со стрелкой и имеющий продолжительность, равную 34 дням, является ложным, поскольку по логике работа 4—6 (монтаж конструкций на I захватке) не зависит от окончания работы 2—3 (отрывка котлована на II захватке). При введении дополнительных событий на сетевом графике (см. рис. 6, б) указанное логическое противоречие устранено, критический путь составляют работы и зависимости между ними 1—2, 2—5, 5—6, 6—9, 9— 10, 10—11, 11—16, 16—17, 17—18 и он равняется 33 дням.
|
|
Рисунок 4 – Сетевой график, построенный по схеме «горизонталь-захватка»: а – неправильное изображение, б – правильное изображение
Как видно из рис. 5, топология данной сетевой модели является ошибочной, так как, например, работа по устройству фундаментов на III захватке (работа 5-7) технологически не зависит от монтажа каркаса на I захватке (работа 3-4) с учётом того, что для производства монтажных работ нулевого цикла и надземной части используются разные грузоподъёмные механизмы. Аналогичная ситуация наблюдается и для работы 7-8, которая технологически зависит лишь от наличия фронта работ по захватке (должна быть закончена работа 5-7) и от загруженности бригады монтажников (необходимо завершение работы 5-6). Между тем на модели прослеживается зависимость начала работы 7-8 от окончания работы 4-6 (кровельные работы на I захватке), что технологически ошибочно.

Рисунок 5 – Сетевой график, построенный по схеме «горизонталь-процесс»: а – неправильное изображение, б – правильное изображение
Для разрешения данного противоречия необходимо по всем захваткам, кроме первой и последней (в данном случае по второй), ввести чередование строительных процессов и фиктивных работ, для чего необходимо введение дополнительных событий (см. рис. 5).
Задание
Разработать топологию сетевого графика. Проверить правильность построения сетевой модели с целью устранения ложных технологических зависимостей, "хвостов", "тупиков", "замкнутых контуров" и, в случае необходимости, скорректировать первоначальный вариант модели. Пронумеровать события, нанести на модель названия работ, их продолжительность, количество занятых рабочих, номер захватки или яруса, на котором выполняется строительный процесс.
Исходные данные для выполнения задания приведены в табл. 1. Подразумевается возведение одноэтажного промышленного здания из сборных железобетонных конструкций, при этом здание делится на захватки в пределах одного температурного блока (в плане). Продолжительность выполнения работ и численность рабочих приведены для одной захватки.
Решить одним из методов : «горизонталь-захватка» или «горизонталь-процесс».
Таблица 1 - Продолжительность выполнения работ на захватке, (дн.) / количество рабочих (человек)
| № варианта | Кол-во захваток | Земляные работы | Устройств о фундаментов | Монтаж надземной части | Заполнение проёмов | Кровельные работы | Санитарно-технические работы | Электротехнические работы | Отделочные работы |
| 13/4 | 11/5 | 16/5 | 8/5 | 11/6 | 9/4 | 10/4 | 14/5 | ||
| 15/4 | 9/5 | 12/5 | 11/5 | 13/5 | 7/4 | 8/5 | 18/4 | ||
| 13/4 | 11/4 | 14/5 | 11/5 | 10/4 | 9/5 | 10/5 | 18/4 | ||
| 15/4 | 12/5 | 16/5 | 9/4 | 11/6 | 8/4 | 7/5 | 15/5 | ||
| 13/3 | 12/4 | 16/5 | 11/5 | 15/4 | 7/4 | 7/4 | 16/5 | ||
| 15/3 | 11/4 | 18/5 | 9/4 | 12/4 | 9/5 | 9/5 | 15/6 | ||
| 15/4 | 11/5 | 16/5 | 8/5 | 13/4 | 9/4 | 10/4 | 15/5 | ||
| 13/4 | 9/5 | 15/5 | 11/5 | 13/5 | 7/4 | 8/5 | 15/5 | ||
| 15/4 | 11/4 | 16/5 | 11/5 | 10/4 | 9/5 | 10/5 | 15/5 | ||
| 13/4 | 12/5 | 16/5 | 9/4 | 9/6 | 8/4 | 7/5 | 15/5 | ||
| 15/3 | 12/4 | 18/5 | 11/5 | 15/4 | 7/4 | 7/4 | 16/5 | ||
| 13/3 | 11/4 | 18/5 | 9/4 | 12/4 | 9/5 | 9/5 | 15/6 | ||
| 15/4 | 11/5 | 16/5 | 11/5 | 11/6 | 9/5 | 10/4 | 14/5 | ||
| 13/4 | 9/5 | 15/5 | 8/5 | 13/5 | 8/4 | 8/5 | 18/4 | ||
| 15/4 | 11/4 | 15/5 | 11/5 | 10/4 | 9/5 | 10/5 | 18/4 | ||
| 15/4 | 12/5 | 18/5 | 11/4 | 11/6 | 8/4 | 7/5 | 16/5 | ||
| 13/3 | 12/4 | 18/5 | 11/5 | 15/4 | 8/4 | 7/4 | 15/5 | ||
| 15/3 | 11/4 | 16/5 | 9/4 | 12/4 | 9/4 | 9/5 | 15/6 | ||
| 13/4 | 11/5 | 16/5 | 8/5 | 11/6 | 9/5 | 10/4 | 14/5 | ||
| 15/4 | 9/5 | 18/5 | 11/5 | 13/5 | 7/4 | 8/5 | 16/4 | ||
| 13/4 | 11/4 | 14/5 | 11/5 | 11/6 | 9/5 | 10/5 | 18/4 | ||
| 15/4 | 12/5 | 12/5 | 11/5 | 11/6 | 7/4 | 7/5 | 15/5 | ||
| 13/3 | 12/4 | 12/5 | 11/5 | 12/4 | 7/4 | 7/4 | 18/5 | ||
| 15/3 | 11/4 | 18/5 | 9/4 | 15/4 | 9/5 | 9/5 | 15/6 | ||
| 13/4 | 11/5 | 16/5 | 8/5 | 12/6 | 9/5 | 10/4 | 16/5 |
Вопросы к практическому занятию
1. Что такое " сетевое планирование"и «сетевые модели»?
2. По каким признакам классифицируются сетевые модели?
3. Назовите и охарактеризуйте основные элементы сетевых графиков.
4. Как обозначается на сетевых графиках его элементы?
5. Что такое критический путь, каковы его признаки?
Рекомендуемая литература: [2, 13, 15, 25, 34, 38].
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 2
Расчет параметров сетевой модели табличным (аналитическим) способом
Теоретическая часть
Основными параметрами сетевых графиков являются:
1. Продолжительность критического пути Ткр — это максимальный по продолжительности путь от исходного до конечного события сетевого графика.
2. Раннее начало выполнения работы  — это самый ранний из всех возможных моментов времени начала работы, обусловливаемый выполнением всех предшествующих работ. Раннее начало исходящей работы (работ) равно нулю. Ранние начала всех последующих работ равны максимальному значению из всех возможных ранних окончаний предшествующих работ, т.е.
— это самый ранний из всех возможных моментов времени начала работы, обусловливаемый выполнением всех предшествующих работ. Раннее начало исходящей работы (работ) равно нулю. Ранние начала всех последующих работ равны максимальному значению из всех возможных ранних окончаний предшествующих работ, т.е.
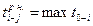 (1)
(1)
3. Раннее окончание выполнения работы 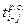 — это самый ранний из возможных моментов времени окончания работы, начатой в самое раннее начало ее выполнения. Оно равно сумме ее раннего начала и продолжительности выполнения, т.е.
— это самый ранний из возможных моментов времени окончания работы, начатой в самое раннее начало ее выполнения. Оно равно сумме ее раннего начала и продолжительности выполнения, т.е.

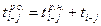 (2)
(2)
Расчет ранних начал и ранних окончаний работ ведут последовательно слева направо от исходного события к завершающему.
4. Позднее начало выполнения работы 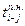 —самый поздний момент времени начала работы, при котором продолжительность критического пути не изменится.
—самый поздний момент времени начала работы, при котором продолжительность критического пути не изменится.
5. Позднее окончание выполнения работы 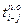 — самый поздний из допустимых моментов времени окончания работы, при котором продолжительность критического пути не изменится. Позднее окончание завершающей работы (работ) равно величине критического пути. Поздние окончания других работ равны минимальному из всех возможных значений позднего начала последующих работ. Позднее и раннее окончания выполнения одной и той же работы между собой связаны зависимостью:
— самый поздний из допустимых моментов времени окончания работы, при котором продолжительность критического пути не изменится. Позднее окончание завершающей работы (работ) равно величине критического пути. Поздние окончания других работ равны минимальному из всех возможных значений позднего начала последующих работ. Позднее и раннее окончания выполнения одной и той же работы между собой связаны зависимостью:
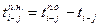 (3)
(3)
Расчет поздних окончаний и поздних начал выполнения работ ведут справа налево от завершающего события сетевого графика к исходному.
6. Общий резерв времени выполнения работы Ri-j равен максимальному количеству времени, на которое можно перенести начало выполнения данной работы или увеличить ее продолжительность без изменения продолжительности критического пути:
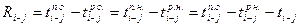 (4)
(4)
7. Частный резерв времени выполнения работы ri-j равен максимальному количеству времени, на которое можно перенести начало выполнения данной работы или увеличить ее продолжительность без изменения раннего начала последующих работ:
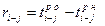 (5)
(5)
Параметры сетевого графика можно рассчитать аналитическим способом, расчёт выполняется в форме таблицы. Рассчитаем параметры сетевого графика, изображенного на рис. 6. данным способом (см. табл. 2).
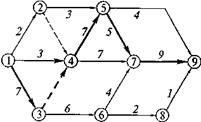 |
Рисунок 6 - Сетевой график производства работ с параметрами, рассчитанными по табл. 2: 1—7, 9 — продолжительность работы, i—j
На начальном этапе необходимо описать исходную сетевую модель. При этом во вторую графу таблицы заносятся шифры всех работ и зависимостей, начиная с работы, выходящей из первого события. Шифры работ должны быть включены в таблицу последовательно, произвольный порядок включения работ и зависимостей в таблицу недопустим. В третью графу таблицы вносятся продолжительности всех работ и зависимостей. Расчёт сетевого графика начинается с определения значений ранних параметров работ. Ранние начала работ 1—2, 1—3, 1—4 равны нулю, а их ранние окончания соответственно:
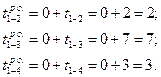
Раннее начало работы 2—5 и фиктивной работы 2—4, как видно из графика на рис. 2, будет равно раннему окончанию работы 1—2, т.е. 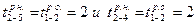 Ранние начала работ 3—6, 4—5, 4—7 и ожидание 3—4 соответствуют раннему окончанию работы 1—3, т.е.
Ранние начала работ 3—6, 4—5, 4—7 и ожидание 3—4 соответствуют раннему окончанию работы 1—3, т.е.
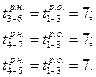
Таблица 2 - Таблица расчета параметров сетевого графика
| Шифр работ, i-j | Продолжительность работ, ti-j | Раннее | Позднее | Резерв времени | |||
Начало работы, 
| Окончание работы, 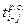
| Начало работы, 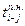
| Окончание работы, 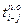
| Общий, Ri-j | Частный, ri-j | ||
| 1-2 | |||||||
| 1-3 | |||||||
| 1-4 | |||||||
| 2-4 | |||||||
| 2-5 | |||||||
| 3-4 | |||||||
| 3-6 | |||||||
| 4-5 | |||||||
| 4-7 | |||||||
| 5-7 | |||||||
| 5-9 | |||||||
| 6-7 | |||||||
| 6-8 | |||||||
| 7-9 | |||||||
| 8-9 | |||||||
Ранние окончания работ 3—6, 4—5, 4—7 будут равны соответственно
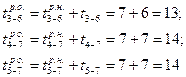
и ожидания 3—4 — 
У работ 5—7 и 5—9 ранние начала будут равны позднему окончанию работы 4—5, т.е.  , а у работ 6—7 и 6—8 — позднему окончанию работы 3—6, т. е.
, а у работ 6—7 и 6—8 — позднему окончанию работы 3—6, т. е. 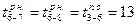
Ранние окончания у работ 5—7 и 5—9 — соответственно 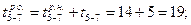 и
и 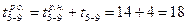 , а у работ 6—7 и 6—8 — соответственно
, а у работ 6—7 и 6—8 — соответственно 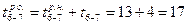 и
и  . Ранние начала работ 7—9 и 8—9 будут равны соответственно ранним окончаниям работ 5—7 и 6—8, т.е.
. Ранние начала работ 7—9 и 8—9 будут равны соответственно ранним окончаниям работ 5—7 и 6—8, т.е. 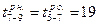 и
и 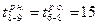 Ранние окончания работ 7—9 и 8—9, входящих в завершающее событие, соответственно
Ранние окончания работ 7—9 и 8—9, входящих в завершающее событие, соответственно 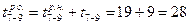 и
и 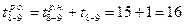 .
.
Максимальное значение раннего окончания работ 7—9 и 8—9, входящих в завершающее событие, равное 28-му дню, определяет продолжительность критического пути, общую продолжительность выполнения всех работ.
По окончании расчета ранних начал и ранних окончаний выполнения работ рассчитываются в таблице поздние начала и поздние окончания выполнения работ. Эти расчеты выполняются в следующей последовательности.
Полученное максимальное значение раннего окончания завершающих работ переносится в графу позднего окончания этих paбот. В графике на рис. 2 это работы 5—9, 7—9 и 8—9. Их поздние и окончания будут равны 28 (см. табл. 1), т. е.
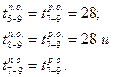
Поздние начала этих работ рассчитывают так:
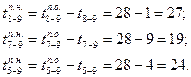
Позднее начало работы 8—9 будет поздним окончанием предшествующей ей работы 6—8, а позднее начало работы 7—9 — поздними окончаниями работ 6—7, 5—7 и 4—7, т.е.
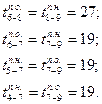
Поздние начала работ 6—8, 6—7, 5—7 и 4—7 — соответственно
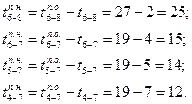
Полученные поздние начала работ будут поздними окончаниями предшествующих им работ. Работе 3—6 предшествуют работы 6—7 и 6—8, у которых ранние начала работ равны соответственно 15-му и 25-му дню. По правилам расчета принимается меньшее значение из возможных. В данном случае оно равно 15, т.е. 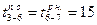 потому что
потому что 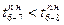 .
.
Работам 5—7 и 5—9 предшествуют работы 2—5 и 4—5, тогда их поздние окончания выполнения 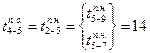 , а поздние начала — соответственно
, а поздние начала — соответственно
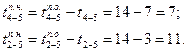
Ожиданиям (фиктивным работам) 3—4 и 2—4 и работе 1—4 предшествуют работы 4—5 и 4—7, тогда их поздние окончания 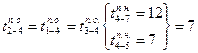 и соответственно этой величине будут равны и поздние начала их выполнения, т. е.
и соответственно этой величине будут равны и поздние начала их выполнения, т. е.
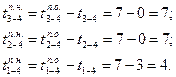
Работе 1—3 предшествуют работы 3—4 и 3—6. Тогда позднее окончание выполнения  , а позднее начало выполнения
, а позднее начало выполнения 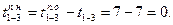
Работе 1—2 предшествуют работы 2—4 и 2—5. Тогда позднее окончание выполнения 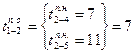 , а позднее начало выполнения
, а позднее начало выполнения 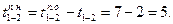
Общие резервы времени выполнения работ определяются по формуле их расчета 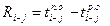 . Например, для работы 6—8 он равен 27 — 15 = 12.
. Например, для работы 6—8 он равен 27 — 15 = 12.
Частные резервы времени выполнения работ определяются как разность между величиной раннего начала последующей работы и раннего окончания данной работы. Так, для работы 6—8 он равен 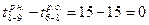 , т.е. его нет.
, т.е. его нет.
Из табл.2 видно, что у работы 1—3, зависимости 3—4, работ 4—5, 5—7, 7—9 общие и частные резервы времени равны нулю. Указанные работы образуют цепочку критического пути.
Задание
Рассчитать параметры сетевого графика в табличной форме по вариантам, работы имеющие продолжительность 0 являются фиктивными (зависимостями).
Таблица 3 – Исходные данные для расчета сетевого графика в табличной форме
| Шифр работ, i-j | Продолжительность работ, ti-j , по вариантам | ||||||||||||||
| 1-2 | |||||||||||||||
| 1-3 | |||||||||||||||
| 1-4 | |||||||||||||||
| 2-4 | |||||||||||||||
| 2-7 | |||||||||||||||
| 3-4 | |||||||||||||||
| 3-6 | |||||||||||||||
| 4-5 | |||||||||||||||
| 4-7 | |||||||||||||||
| 5-6 | |||||||||||||||
| 5-8 | |||||||||||||||
| 6-8 | |||||||||||||||
| 7-8 | |||||||||||||||
| 8-9 | |||||||||||||||
| Шифр работ, i-j | Продолжительность работ, ti-j , по вариантам | ||||||||||||||
| 1-2 | |||||||||||||||
| 1-3 | |||||||||||||||
| 1-4 | |||||||||||||||
| 2-4 | |||||||||||||||
| 2-7 | |||||||||||||||
| 3-4 | |||||||||||||||
| 3-6 | |||||||||||||||
| 4-5 | |||||||||||||||
| 4-7 | |||||||||||||||
| 5-6 | |||||||||||||||
| 5-8 | |||||||||||||||
| 6-8 | |||||||||||||||
| 7-8 | |||||||||||||||
| 8-9 | |||||||||||||||
Вопросы к практическому занятию
1. Какие параметры определяются при расчете сетевых модолей?.
2. Каков порядок расчета ранних параметров работ при применении аналитического способа?
3. Каков порядок расчета поздних параметров работ при применении аналитического способа?
4. Как рассчитать резервы времени работ, используя аналитический метод расчета?
Рекомендуемая литература: [2, 13, 15, 25, 34, 38].
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3
Расчет параметров сетевого графика непосредственно на его поле в секторной форме
Теоретическая часть
На практике применяются сетевые графики с расчетом временных параметров непосредственно на них. Часто используется секторная форма отображения параметров непосредственно на сетевых графиках.
 |
При секторной форме отображения параметров сетевых графиков кружки, обозначающие события, следует разделить на четыре сектора, как это показано на рис. 7. В верхних секторах кружков проставляются номера событий сетевого графика. В левых секторах проставляются ранние начала входящих в них (предшествующих) работ, а в правых секторах — поздние окончания выходящих из них (последующих) работ. В нижнем секторе проставляется номер события, из которого в данное событие ведет максимальный путь. Иногда нижний сектор не заполняют.
Сначала на графике рассчитываются ранние начала выполнения работ, т. е. заполняются левые сектора кружков. Расчет ведется от начального события слева направо к конечному событию. В левый сектор исходного события записывается «0», так как ранние начала работ, выходящих из этого события, всегда равны нулю. Поскольку у исходящих из верхнего сектора нет предшествующих работ, в нижнем секторе также записывается «0». Далее последовательно рассчитываются ранние начала всех последующих работ и заполняются левые секторы последующих кружков-событий.
На рис. 8 приведен расчет сетевого графика непосредственно на нем в секторной форме.
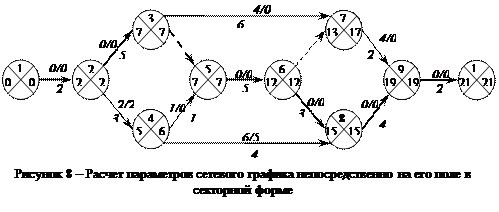
Раннее начало работ, выходящих из события, равно максимальному раннему окончанию работ, входящих в него, т. е. максимальной из возможных сумм раннего начала и продолжительности входящих (предшествующих) в событие работ. Ранние начала работ 2—3 и 2—4 для сетевого графика будут равны 0 + 2 = 2. В левом секторе кружка-события 2 записывается значение 2. Далее, раннее начало работы 3—7 и ожидания 3—5 будет равно 2 + 5 = 7, а работ 4—8 и 4—5 — 2 + 3 = 5. Эти значения вписываются в левые сектора кружков-событий 3 и 4. Ранним началом работы 5—6 будет максимальное значение из выражений 7 + 0 = 7 и 3 + 1=4, т.е. 7-й день. Это значение записывается в левый сектор кружка-события 5. Аналогичным образом рассчитываются ранние начала для всех работ, исходящих из последующих кружков-событий. Для кружка-события 6 оно равно 7 + 5 = 12, для кружка-события 7 берется максимальное из двух значений 7 + 6 = 13 и 12 + 0 = 12, т. е. 13-й день. Для кружка-события 8 раннее начало выходящей работы 8—9 принимается равным максимальному значению из величин 12 + 3 = 15 и 6 + 4 = 10, т. е. 15-му дню. Для кружка-события 9 раннее начало выходящей из него работы 9—10 будет равно максимальному значению из трех величин 13 + 2= 15, 12 + 4= 16 и 15 + 4= 19, т.е. 19-му дню. Для последнего кружка-события 10 в левый сектор вписывается значение равное 19 + 2 = 21 как сумма раннего начала работ, предшествующих завершающей работе 9—10, и ее продолжительности, равной 2.
Раннее наступление события 10 по смыслу и простой логике является также и поздним окончанием всех работ. Поэтому в завершающем событии значение в левом секторе переносится в правый сектор и начинается расчет поздних окончаний других работ и заполнение правых секторов кружков.
Расчет поздних окончаний работ и заполнение правых секторов кружков-событий ведется последовательно справа налево. Позднее окончание работ, входящих в кружок-событие 9, будет равно 21 - 2 = 19. Поздние начала работ, исходящих из кружков-событий 7 и 8 будут равны соответственно 19-2 = 17 и 19-4=15. Для работ, исходящих из кружка-события 6, раннее начало выбирается как минимальное из значений 17— 0, 19 - 4 = 15 и 15 - 3 = 12, т. е. 12-й день. Раннее начало работы, исходящей из кружка-события 5, будет равно 12-5 = 7. Для работ, выходящих из кружка-события 4, раннее их начало принимается минимальным из значений 15 - 4 = 11 и 7 - 1 = 6, т. е. 6-й день. Раннее начало работы 3—7 определится как минимальное из величин 17-6 = 11 и 7-0 = 7, т.е. 7-й день. Раннее начало работ, выходящих из кружка-события 2, будет минимальным из выражений 6-3 = 3 и 7-5 = 2, т. е. 2-й день. Раннее окончание исходящего события должно быть равно нулю, и по расчету оно 2-2 = 0, что свидетельствует об отсутствии ошибок в проведенном расчете. Если при расчете значение величины правого сектора исходящего события не равно нулю, расчеты необходимо повторить вновь.
По рассчитанным значениям параметров в левых и правых секторах определяется критический путь. Он проходит через события, у которых значения параметров в левом и правом секторах одинаковы. У графика на рис. 9, а к событиям, лежащим на критическом пути, относятся кружки-события 1—3, 5, 6, 8—10.
Рассчитанных на графике значений в правых и левых секторах достаточно, чтобы знать ранние и поздние начала и ранние и поздние окончания всех работ. Так, раннее начало работы 7—9 равно значению левого кружка-события 7, т.е. 13-му дню. Если к нему прибавить продолжительность работы, т. е. 13 + 2 = 15, то это будет ее ранним окончанием. Позднее окончание этой работы равно значению правого сектора кружка-события 9, т.е. 19-му дню. Если из него вычесть продолжительность работы, то это будет ее самым поздним началом, т.е. 19-2 = 17 или 17-й день.
После расчета ранних начал работ, исходящих из событий, и поздних окончаний работ, входящих в события, рассчитывают и наносят на сетевой график общий и частный резервы времени выполнения работ. Они рассчитываются по формулам
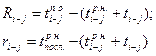
где  — раннее начало выполнения последующих работ.
— раннее начало выполнения последующих работ.
Так, для работы 4—8 общий резерв времени ее выполнения R
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|