СВОЙСТВА ПЛАНА УСКОРЕНИЙ

§ 7 СВОЙСТВА ПЛАНА УСКОРЕНИЙ

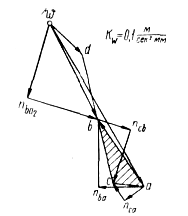
1. Из схемы механизма (рис. 2) и плана ускорений (рис. 5) устанавливаем, что план ускорений, как и план скоростей, обладает изображающими свойствами. Сравним ê ABD и ê abd на указанных чертежах. Эти треугольники будут подобны и сходственно расположены, так как все их стороны оказываются повернутыми против часовой стрелки на один и тот же угол 180°—q₂. Угол q₂ определяется равенством

tg q₂ = 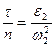. (50)

Действительно, 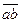на плане ускорений образует угол q₂ с 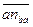, так как

tg q₂ =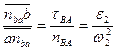

Отрезок an_ba параллелен АВ ê ADB на схеме механизма. Следовательно, угол между стороной АВ и отрезком 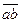будет также q₂ и можно считать, что 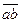на плане ускорений повернут против часовой стрелки на угол 180°— q₂ относительно направления АВ. Рассуждая аналогичным образом, находим, что стороны bd и da треугольника плана ускорений повернуты против часовой стрелки на угол 180°— q₂ по отношению к сторонам BD и DA ê ABD на схеме механизма. Таким образом, теорема подобия для точек жестких звеньев механизма справедлива и для плана ускорений. Это положение значительно упрощает нахождение ускорений точек механизма. Так, например, имея отрезок 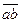на плане ускорений, достаточно на нем построить подобный и сходственно расположенный ê abd и мы найдем ускорение точки d, соединив полюс w плана ускорений с вершиной d построенного треугольника. Этим самым уравнения (33) и (34), применявшиеся для нахождения ускорения точки D, становятся лишними.

Построив план ускорений для точек А, В и С механизма, изображенного на рис. 4, а, на основании теоремы подобия легко найдем ускорение и точки D (рис. 6). Имея ê abc, построенный в соответствии с правилами, изложенными в предыдущем параграфе, продолжим отрезок 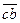за точку b и отложим на проведенной прямой отрезок 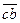, который найдем из пропорции

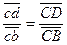Соединив точку d с полюсом w, определим отрезок 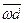, исходящий из полюса плана скоростей, который и будет изображать по величине и направлению ускорение точки D в выбранном масштабе .

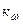На основании вышеизложенного первое свойство плана ускорений можно сформулировать так: каждое подвижное звено механизма изображается на плане ускорений, одноименным подобным и сходственно расположенным контуром, повернутым на некоторый угол 180°—q относительно соответствующего звена механизма.

2. Все неподвижные шарниры механизма изображаются полюсом плана ускорений. Звенья механизма, вращающиеся вокруг неподвижных шарниров, изображаются на плане ускорений одноименными отрезками, исходящими из полюса и являющимися векторами абсолютных ускорений данных точек. Отрезки плана ускорений, соединяющие концы векторов абсолютных ускорений, являются полными относи тельными ускорениями, направления которых определяются правилом геометрического сложения нормальных и касательных их составляющих.

Рис.6.План ускорений механизма Рис.7. Определение величины радиуса

изображенного на рис.4,а. кривизны траектории точки D.

3. Полюс плана ускорений изображает и все мгновенные центры ускорений звеньев механизма в данный момент времени. Чтобы найти, например, положение мгновенного центра ускорений звена 2 на схеме механизма (рис. 2), достаточно на его стороне АВ построить треугольник, подобный и сходственно расположенный с ê abw плана ускорений. Тогда вершина треугольника, находящаяся против стороны АВ звена 2, будет являться мгновенным центром ускорений звена 2.

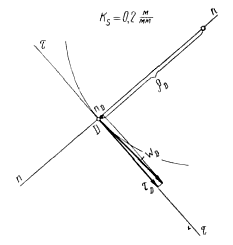
4. Используя совместно планы скоростей и ускорений, можно найти радиусы кривизны траекторий точек механизма. Так, например, найдя ускорение W_D по величине и направлению, разложим его на две составляющие t_D и п_D — по скорости и перпендикулярно к ней (рис. 7), т. е. по нормали. Так как

n_D = 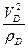, (51)

где r_D—искомый радиус кривизны траектории точки в данный момент,

r_D = 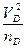. (52)