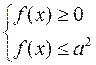- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Иррациональные неравенства и способы их решения
Иррациональные неравенства и способы их решения
 Решение простейших иррациональных неравенств
Решение простейших иррациональных неравенств
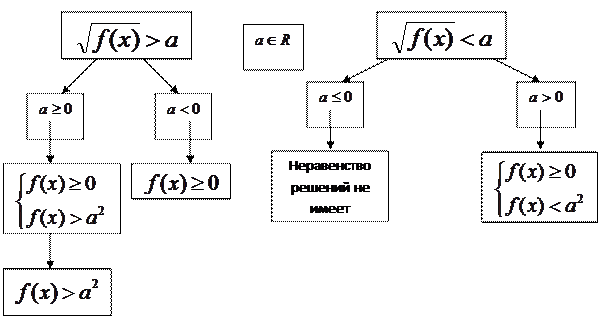

|
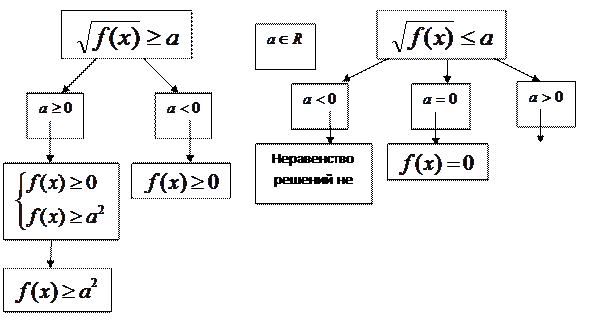
Например:
1) Решите неравенство: 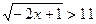 .
.
Решение: 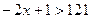 ;
;
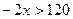 ;
;
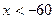 .
.
Ответ: 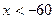 .
.
2) Решите неравенство:  .
.
Решение: 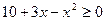 ;
;
решим квадратное уравнение  ;
;
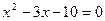 ;
;
 по теореме, обратной теореме Виета:
по теореме, обратной теореме Виета:

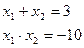


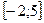
Ответ: 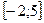 .
.
3) Решите неравенство:  .
.
Решение: 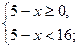
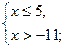
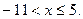
Ответ: 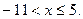
4) Решите неравенство: 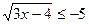 .
.
Решение: т.к. арифметическим корнем четной степени является неотрицательное число, то данное неравенство решений не имеет.
Ответ: неравенство решений не имеет.
5) Решите неравенство: 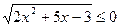 .
.
Решение: 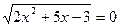 ;
;
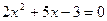 ;
;
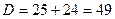 ;
;
 ;
;
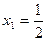 ;
; 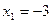 .
.
Ответ: 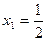 ;
; 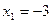 .
.

Решение неравенств:
1) Задания для классной работы:
1. №166-№169(нечетн.) [1, с.66];
2. № 172-173(нечётн.) [1, с.67];
3.  ;
;
4. 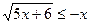 ;
;
5. 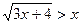 ;
;
6. 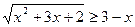 ;
;
7. 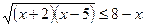 ;
;
8. 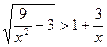 .
.
2) Задания для домашней работы:
1. №166-№169(четн.) [1, с.66];
2. № 172-173(чётн.) [1, с.67];
3. 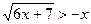 ;
;
4. 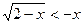 ;
;
5. 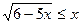 ;
;
6.  ;
;
7. 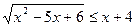 .
.
Контрольная работа: «Иррациональные уравнения и неравенства»
Вариант I
1. Решите уравнения:
а) 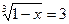 ; д)
; д) 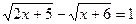 ;
;
б) 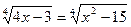 ; е)
; е) 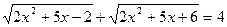 ;
;
в)  ; ж)
; ж) 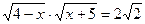 .
.
г)  ;
;
2. Решите неравенства:
а) 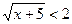 ; в)
; в) 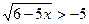 ;
;
б) 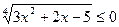 ; г)
; г) 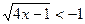 .
.
Вариант II
1. Решите уравнения:
а) 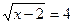 ; д)
; д) 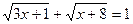 ;
;
б)  ; е)
; е) 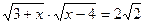 ;
;
в) 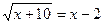 ; ж)
; ж) 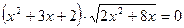 .
.
г) 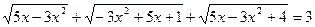 ;
;
2. Решите неравенства:
а) 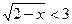 ; в)
; в) 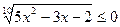 ;
;
б) 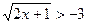 ; г)
; г)  .
.
Литература
1. «Алгебра и начала анализа 10-11» Ш.А. Алимов и др. – 11-е изд. – М.: Просвещение, 2003. – 384 с.
2. «Дидактические материалы по алгебре и началам анализа для 10 класса общеобразовательных учреждений» М.И. Шабунин и др. – М.: Просвещение, 2006. – 189 с.
3. «Иррациональные уравнения и неравенства» А.Х. Шахмейстер – 2 изд. – СПб.: ЧеРо-на-Неве, 2004. – 192 с.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|