- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
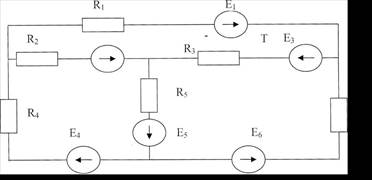
Метод контурнурных токов
Задача №1
Вариант №3
|
Дано:
R1= R2= R3= R4= R5= R6= R=30 Ом
Е3=150 В
Е4=50 В
По 1-му закону Кирхгофа:
 I2+I4-I1=0 (узел а)
I2+I4-I1=0 (узел а)
 I3-I2-I5=0 (узел b)
I3-I2-I5=0 (узел b)
 I5-I4-I6=0 (узел c)
I5-I4-I6=0 (узел c)
 По 2-му закону Кирхгофа:
По 2-му закону Кирхгофа:
I1R1+I3R3+I2R2=E3
I5R5 +I4R4+I2R2=E5
I3R3+I5R5+I6R6=E3+E5
1. Метод контурнурных токов
I11R11-I22R12-I33R13=E3
-I11R21+I22R22-I33R33=E4
-I11R31-I22R32+I33R33=-Е3
где
 R11=R1+R2+R3
R11=R1+R2+R3
R22=R2+R4+R5 собственные сопротивления контуров 1,2,3.
R33=R3+R5+R6
 R12=R21-R2
R12=R21-R2
R13=R31=R3 межконтурные сопротивления
R23=R32=R5
Решая эту систему уравнений, находим контурные токи. Затем вычисляем токи в ветвях.
I1-I11
I5=I22-I33; I6=-I33
2. Метод узловых потенциалов.
В схеме 4 узла. Один из них (узел d) принимаем за базовый, потенциал которого полагаем равным нулю. Для нахождения потенциалов остальных узлов φа, φb, φc заменим системой уравнений:
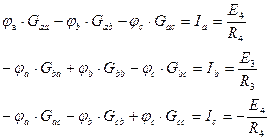
где
|
|
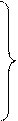
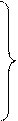 где
где 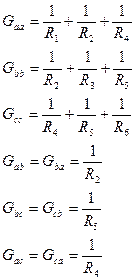
Ia, Ib, Ic – узловые токи а, b и с.
Решая систему уравнений, находим потенциалы узлов a, b и с.
Затем находим токи в ветвях по формулам:

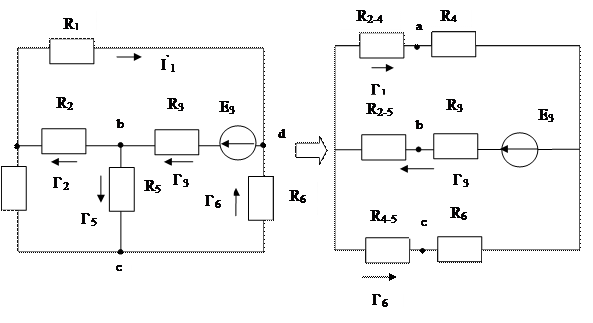
3. Предварительно преобразовав треугольник сопротивлений в звезду, определяем токи в преобразованной схеме методом наложения.
Этот метод заключается в том, что определяются частичные токи в двух схемах, в каждой из которых оставляют по одному источнику ЭДС.
Рассмотрим эти схемы и найдем частичные токи.
1)
|
|
Находим сопротивление звезды:
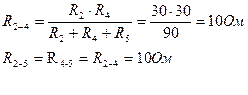
Сопротивление ветвей:
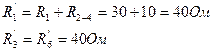
Общее сопротивление цепи: 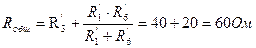
Токи в ветвях: 

2)
|
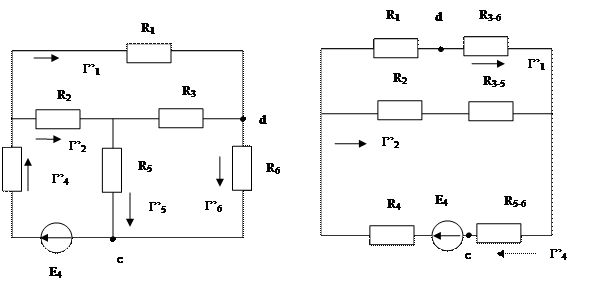
В этой схеме заменяем т-к сопротивление R3R5R6 эквивалентной звездой.
Общее сопротивление цепи такое же, что и в предыдущей схеме.
Токи в ветвях: 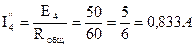
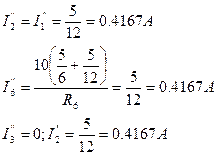
Алгебраическим сложением (с учетом направления частичных токов) находим токи в ветвях заданной схемы:
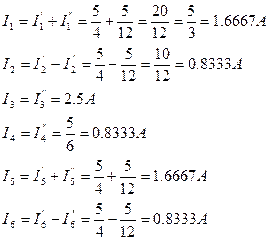
Примечание: Значение токов проверены с помощью составления баланса мощностей.
Определим ток в ветви с резистором R3 метод эквивалентного генератора.
Разрываем ветвь с резистором R3 и находим напряжение на ее зажимах в режиме холостого хода.
| |||||||
 | |||||||
 | |||||||
| |||||||
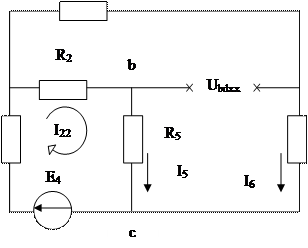
Методом контурных токов находим токи в ветвях I5x и I6x
Cоставим 2 уравнения по второму закону Кирхгофа:
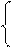
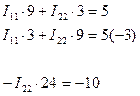
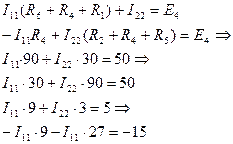
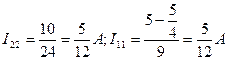
Токи в ветвях:
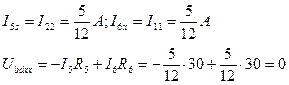
|
| |||||
 | |||||
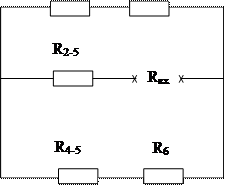 | |||||
Для упрощения схемы заменим т-к сопротивлений R2R4R5 эквивалентной звездой.
Сопротивление звезды
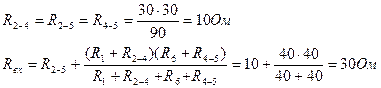
где 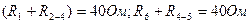
Искомый ток 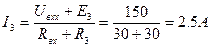
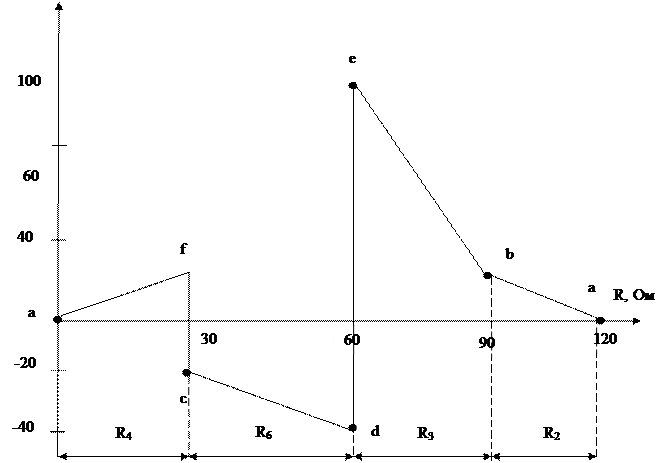
Для контура abedmcfa находим потенциалы точек. Против часовой стрелки, начиная с точки а:
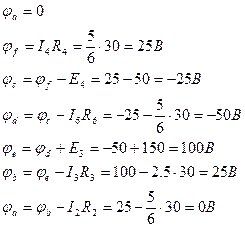
| |||
 | |||
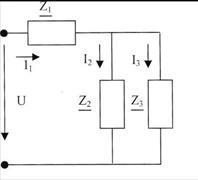
Задача №2.
|
|
Дано:
Ů=10В
z1=j1Ом
z2=2Ом
z3=-j3Ом
Методом комплексных амплитуд найдем ток İ2
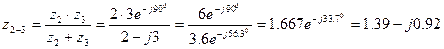
Полное сопротивление всей цепи:
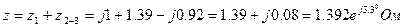
Комплексное амплитудное значение токов и напряжение:
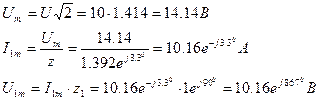
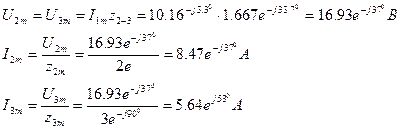
Мгновенное значение тока i2(ωt)=8.47 sin(ωt-370).
Построим зависимость тока i2 от времени.
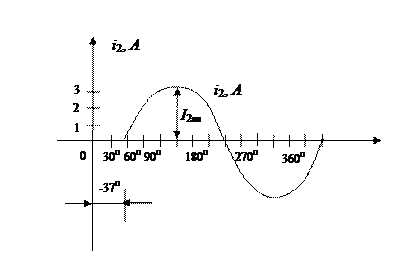
Для построения потенциальной диаграммы напряжений обходим контур abca против часовой стрелки и вычисляем потенциалы точек приняв φа=0.

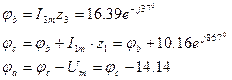
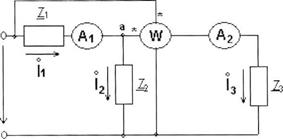 2.
2.
Дано:
IA2=1A
z1=5Ом
z2=10Ом
z3=j10Ом
По условию IA2=1A, полагаем, что İ3=1А
|
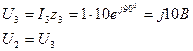
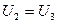
|

Напряжение на зажимах цепи:
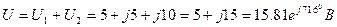
Показание ваттметра:
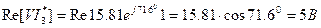
Составим баланс мощностей.
Находим полную комплексную мощность источника.
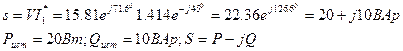
Активная и реактивная мощность потребителей:
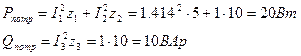
Баланс активной и реактивной мощности выполняется 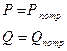
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|