Эконометрика. Задание №1.

Эконометрика

Контрольная работа

Задание №1.

Имеются статистические данные о росте, весе и объеме талии слушателей группы. Определить средние рост, вес и объем талии в группе. Оценить смещенную и несмещенную оценку дисперсии и среднеквадратического отклонения статистических данных биометрических параметров. Построить ковариационную и корреляционную матрицу для роста, веса и объема талии. Найти коэффициенты парных линейных регрессий зависимости объема талии от веса и от роста.

См Задача1.xls

Задание №2 (Зависимость спроса на товар от суммарного дохода)

Использование линейного регрессионного анализа в случае нелинейной зависимости от переменной X и линейной зависимости от параметров.

Зависимость спроса на товар Y от суммарного дохода X определяется кривыми Энгеля. В частности, вида

Y = b0 + b1/X+u,

Y=b0X^b1

где Y -ежегодное потребление бананов семьёй (спрос на товар) фунт/чел,

X -среднегодовой доход семьи на одного человека (суммарный доход) $10тыс.

u - случайная погрешность.

Требуется по статистическим данным оценить параметры b0, b1.

По информационным критериям выбрать лучшую модель.

Найти элластичность

См Задача2.xls

Задание № 3.Для исходных данныхзадачи № 1 построить множественную линейную модель зависимости объема талии от веса роста. Проверить значимость коэффициентов множественной регрессии. Как изменится качество модели, если в ней учесть нелинейность, добавив в модель квадратичную от обоих факторов?

См. Задача1.xls

Задание № 4.Для условий задания № 1 определить значения коэффициентов частной корреляции. Сравнить значения коэффициентов парной и коэффициентов частной корреляции. Проверить коллинеарность факторов с помощью анализа значений коэффициентов корреляции, а также определения значения определителя корреляционной матрицы. Проанализировать наличие ложной корреляции между факторами и откликом

См. Задача1.xls

Задание № 5. (нелинеаризуемая нелинейная модель)

Построение нелинейной нелианеризуемой модели.

Решить задачу построения парной регрессии с использованием пакета «Поиск решения», если модель имеет вид

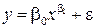Построить модель при допущении о мультипликативной ошибке путем линеаризации теоретической модели регрессии

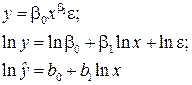
См. Задача5.xls