
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Компланарные векторы. Правило параллелепипеда.
Компланарные векторы. Правило параллелепипеда.
Разложение вектора по трем некомпланарным векторам
Автор: © 2015, ООО КОМПЭДУ, http://compedu.ru
Описание:
При поддержке проекта http://videouroki.net
Задание 1
Вопрос:
Чему равно значение коэффициента x в разложении вектора 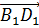 по векторам
по векторам 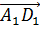 ,
, 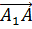 и
и 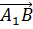 . В ответе укажите только число.
. В ответе укажите только число.
Изображение:
Запишите число:
___________________________
Задание 2
Вопрос:
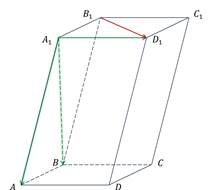
Пользуясь данными рисунка, установите, в каком из пунктов верно найдена сумма векторов.
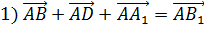
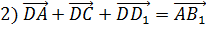
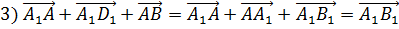
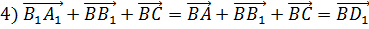
В ответе укажите только число (номер выбранного пункта).
Запишите число: ___________________________
Задание 3
Вопрос:
Какого правила сложения векторов не существует?
Выберите один из 4 вариантов ответа:
1) правила трапеции
2) правила параллелепипеда
3) правила треугольника
4) правила параллелограмма
Задание 4
Вопрос:
Известно, что векторы 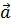 ,
, 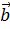 и
и 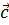 компланарны, а векторы
компланарны, а векторы 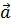 и
и 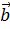 неколлинеарны. Какое из равенств будет тождественным для тройки векторов
неколлинеарны. Какое из равенств будет тождественным для тройки векторов 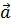 ,
, 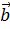 и
и 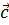 ?
?
Выберите один из 3 вариантов ответа:
1) 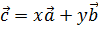 2)
2) 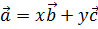 3)
3) 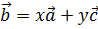
Задание 5
Вопрос:
Пользуясь данными рисунка, укажите тройки компланарных векторов.
Изображение:
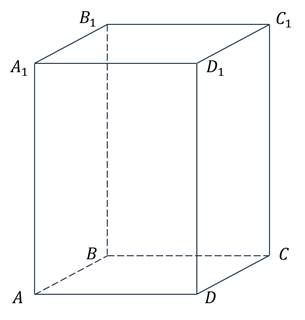
Выберите несколько из 4 вариантов ответа:
1) 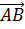 ,
, 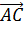 ,
, 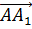
2) 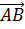 ,
,  ,
, 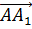
3) 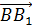 ,
, 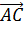 ,
, 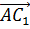
4) 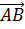 ,
, 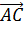 ,
, 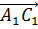
Задание 6
Вопрос:
Пользуясь данными рисунка, укажите разложение вектора 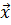 по векторам
по векторам 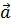 ,
, 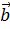 и
и 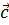 .
.
Изображение:
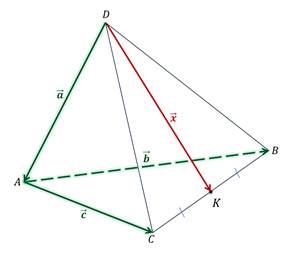
Выберите один из 3 вариантов ответа:
1) 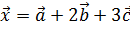
2) 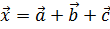
3) 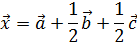
Задание 7
Вопрос:
Чему равно значение коэффициента x в разложении вектора 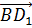 по векторам
по векторам 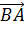 ,
, 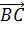 и
и 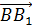 . В ответе укажите только число.
. В ответе укажите только число.
Изображение:
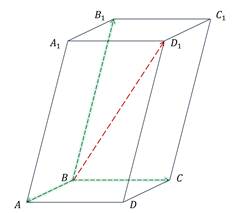
Запишите число:
___________________________
Задание 8
Вопрос:
"Любой вектор пространства можно разложить по трём ... векторам, причём коэффициенты разложения определяются единственным образом."
Какое слово пропущено? Ответ укажите в форме Д.п. и мн.ч.
Запишите ответ:
__________________________________________
Задание 9
Вопрос:
Пользуясь данными рисунка, по правилу параллелепипеда найдите вектор суммы данных векторов.
Изображение:
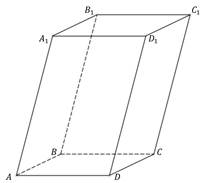
Укажите соответствие для всех 3 вариантов ответа:
1) 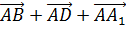
2) 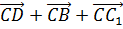
3) 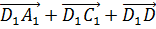
__ 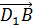
__ 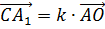
__ 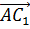
Задание 10
Вопрос:
Укажите верные утверждения.
Выберите несколько из 4 вариантов ответа:
1) Векторы называются компланарными, если при откладывании их от одной и той же точки они не будут лежать в одной плоскости.
2) Векторы называются компланарными, если имеются равные им векторы, не лежащие в одной плоскости.
3) Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
4) Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|