Контакты

Случайная статья

Пусть А- некоторое событие . Тогда противоположное событие, состоящее из всех элементарных исходов, не входящих в событие А.

№ 21

В дальнейшем хорошая деталь – это окрашенная деталь.

Хорошие Плохие

3 2

I.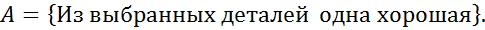

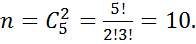
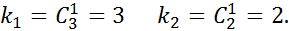
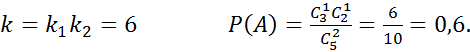
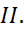
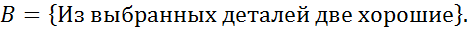
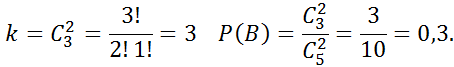
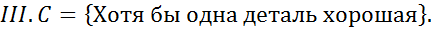
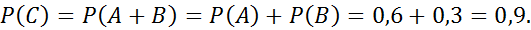
Предварительные сведения.

Пусть имеется некоторый эксперимент; E- пространство элементарных исходов.

Противоположное событие.

Пусть А- некоторое событие . Тогда противоположное событие, состоящее из всех элементарных исходов, не входящих в событие А.

Произведение событий.

Пусть А и В - некоторые события. Произведением событий 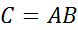называется событие, состоящее из элементарных исходов, входящих и в событие А, и в событие В одновременно.

Сумма событий.

Пусть А и В - некоторые события. Суммой событий 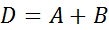состоит из элементарных исходов, входящих или в событие А, или в событие В.

Несовместные события.

События А и В называются несовместными, если они не имеют общих элементарных исходов; т.е.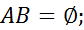

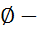пустое множество.

Аксиомы теории вероятностей.

1.

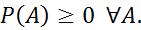
2. 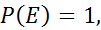где E- достоверное событие.

3. 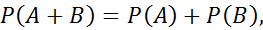если А и В - несовместные события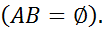

Следствие.

1.

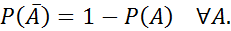
2.

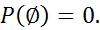
3.

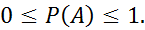
Независимые события.

События А и В называются независимыми, если

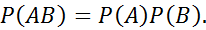
№ 51

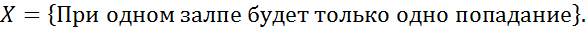
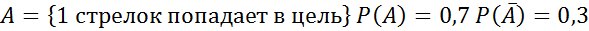
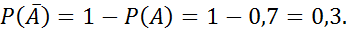
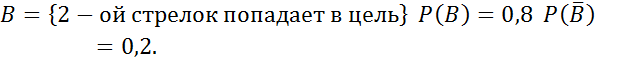
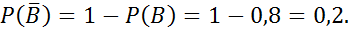
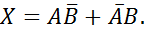
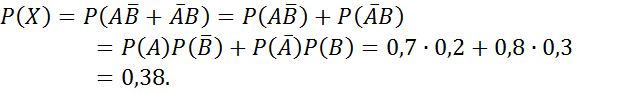
№ 56 (а,б)

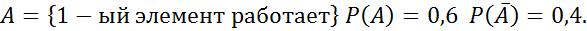
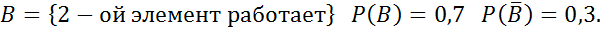
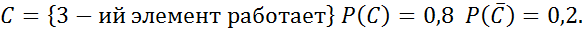
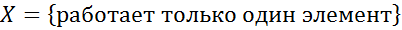
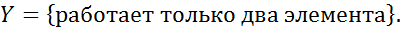
Решение.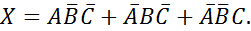

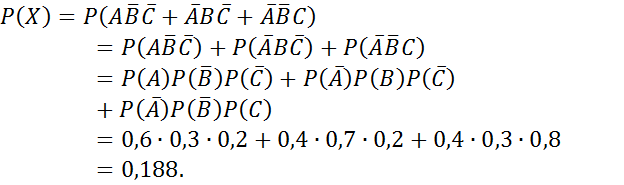
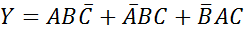
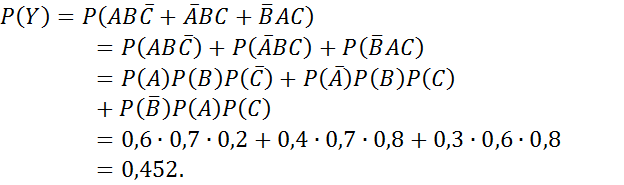
Вероятность появления хотя бы одного события.

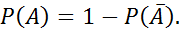
№80

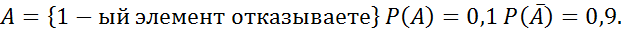
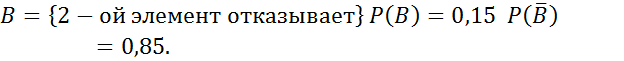
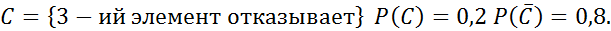
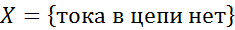
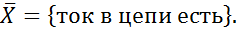
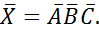
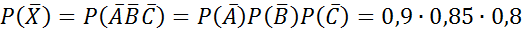
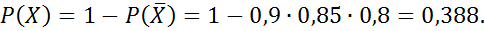
№82

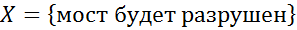
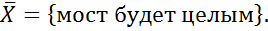
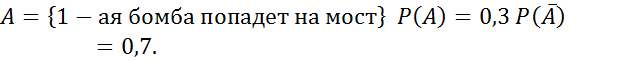
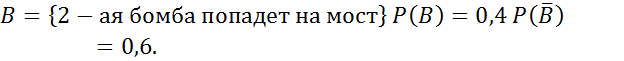
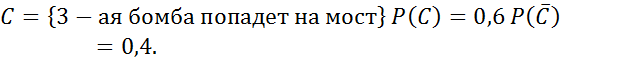
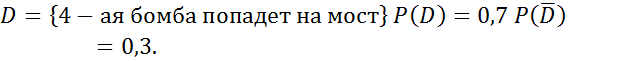
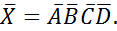
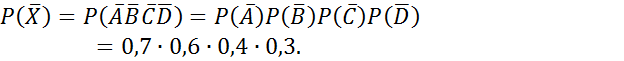
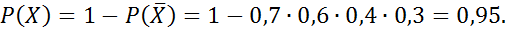
Условная вероятность.

При любых событиях А и В выполняется равенство

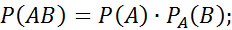
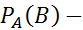условная вероятность появление события В при условии, что событие А произошло.

№64

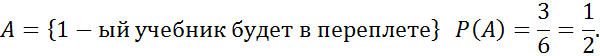
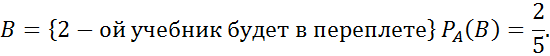
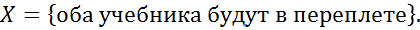
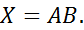
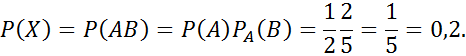
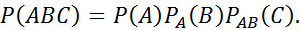
№66

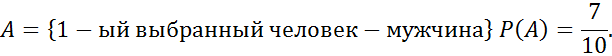
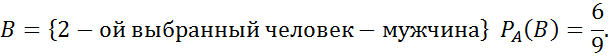
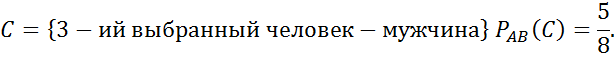
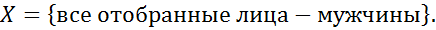
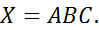
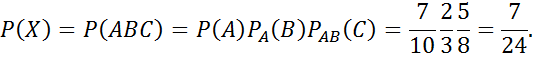
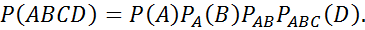
№67

Окрашенных деталей Неокрашенных

6 4

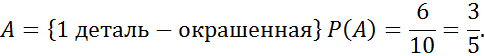
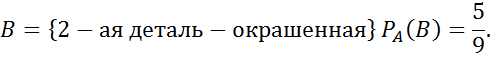
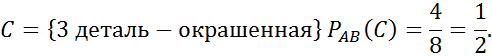
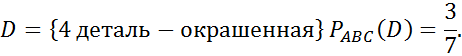
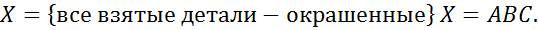
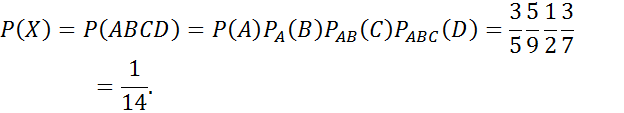
На дом: В.Е. Гмурман «Руководство к решению задач по теории вероятностей и математической статистике».

№№ 50 56(в) 61 81 65 69

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.