
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Формула полной вероятности. Формула Байеса
Классическое определение вероятности: Вероятность события А равна отношению числа случаев, благоприятствующих ему (m), к общему числу возможных случаев (n):
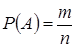 .
.
Размещения из n (всех) элементов по m называются комбинации, отличающиеся друг от друга не только составом элементов, но и их расположением или и тем, и другим.
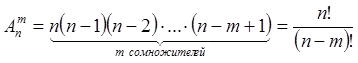 .
.
Замечание: Если при упорядоченной выборке m элементов из n, элементы возвращаются обратно, то полученные выборки называются размещением с повторением.
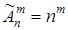
Задача. В лифт на 1–ом этаже девятиэтажного дома вошли 4 человека, каждый из которых может выйти на любом этаже со 3–го по 9–ый. Какова вероятность того, что все пассажиры выйдут:
а. на 6–ом этаже;
б. на одном этаже;
в. на разных этажах;
а. Пусть событие А={все вышли на 6–ом этаже}
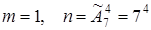 или
или 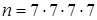 (т.к. каждый пассажир может выйти 8–ю способами), то
(т.к. каждый пассажир может выйти 8–ю способами), то 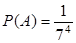
б. Пусть событии В={все вышли на одном этаже}
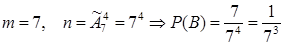
в. Пусть событие С ={все вышли на разных этажах}
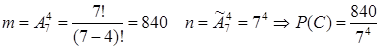
Сочетания из n (всех)элементовпо m называются комбинации из n элементов по m отличающихся друг от друга только составом элементов.
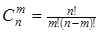
Перестановкой из n элементов называются комбинации, отличающиеся друг от друга только порядком элементов:
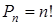 .
.
Замечание: Если среди n элементов имеется k групп, состоящих из одинаковых элементов, причем элементы в 1-й группе повторяются раз, во 2-ой раз, … , в k –ой раз, причём , такие перестановки называются перестановки с повторением
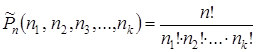
Задача. В лотереи 6 из 45, выигрывает тот, кто угадал 4, 5 или 6 номеров. Найти вероятность того, что угаданы:
а. 6 цифр;
б. 4 цифры.
а. Пусть событие А={угадано 6 цифр}.
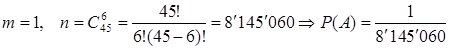
б. пусть событие В={угадано 4 цифры}, т.е. 4 цифры угаданы и 2 цифры не угаданы
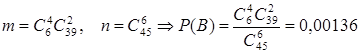
Задача. В партии 100 изделий, из которых 4 шт. бракованные. Партию произвольным образом разделили пополам и отдали двум покупателям. Определить вероятность того, что бракованные изделия достались:
а. одному покупателю;
б. обоим покупателям поровну.
а. пусть событие А={вест брак достался одному}, т.е. ему досталось 4 бракованные изделия и 46 не бракованных, а второму все 50 не бракованных.
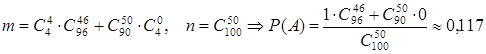
б. пусть В={брак разделился поровну}
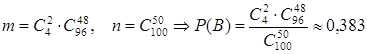
Задача. В магазине было продано 21 из 25 холодильников трех марок, имевшихся в количестве 5, 7 и 13 штук. Полагаем, что все холодильники равноценных марок и стоимости. Найти вероятность того, что оставшиеся холодильники:
а. одной марки;
б. трех марок.
а. Пусть событие А={остались холодильники одной марки}
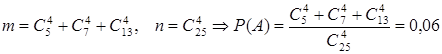
б. пусть событие В={остались холодильники трех марок}
Остаток возможен в 3–х вариантах:
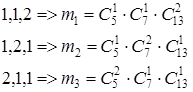
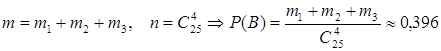
Вероятность появления хотя бы одного события.
Задача. Устройство содержит два независимо работающих элемента, вероятности отказов, которых, соответственно 0,05 и 0,08. Найти вероятность отказа устройства, если для этого достаточно отказа одного элемента
Пусть событие 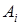 ={отказ i–го элемента}
={отказ i–го элемента}
В={отказ устройства}
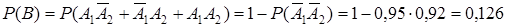
Задача. Среди билетов денежно–вещевой лотереи ровно половина выигрышных. Сколько билетов нужно купить, чтобы с вероятностью 0,999 быть уверенным в выигрыше хотя бы по одному билету.
Пусть событие 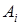 ={выигрыш по i–му билету}, тогда P(
={выигрыш по i–му билету}, тогда P( 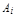 )=0.5, т.к половина билетов выигрышная.
)=0.5, т.к половина билетов выигрышная.
1. вероятность выигрыша хотя бы по одному билету есть:
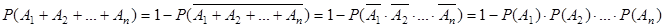
но вероятность выигрыша и не выигрыша по отдельно взятому билету одинакова, в силу условия, поэтому
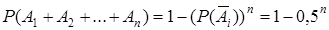
2. 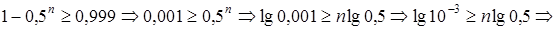
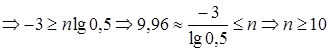
Задача. Вероятность того, что студент сдаст первый экзамен 0,9; второй – 0,9; а третий – 0,8. Найти вероятность того, что студент сдаст:
а) только 2–й экзамен;
б) только один экзамен;
в) три экзамена;
г) по крайней мере, два экзамена;
д) хотя бы один.
Пусть событие 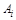 ={студент сдал i экзамен}
={студент сдал i экзамен}
а. Пусть событие В={студент сдал только 2–й экзамен}
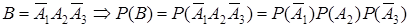
В силу несовместности и независимости этих событий:
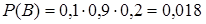
б. Пусть событие С={студент сдал только один экзамен}
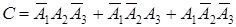
В силу несовместности и независимости этих событий
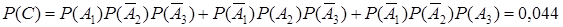
в. Пусть событие D={студент сдал три экзамена}
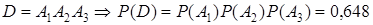
г. Пусть событие E={по крайней мере, два экзамена}
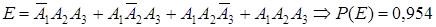
д. Пусть событие F={студент сдал хотя бы один экзамен}
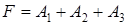
В силу того, что события 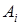 совместны, проще будет найти вероятность противоположного события
совместны, проще будет найти вероятность противоположного события 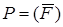 и вычислить его вероятность.
и вычислить его вероятность.
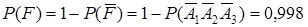
Задача. Причиной разрыва в электросети служит выход из строя первого или одновременно второго и третьего предохранителей. Предохранители независимы и могут выйти из строя с вероятностями 0,1; 0,2 и 0,3. Какова вероятность разрыва сети?
Пусть событие 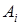 ={выход из строя i предохранителя}
={выход из строя i предохранителя}
событие В={разрыв сети}
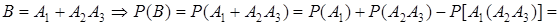
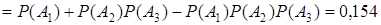
Пример. У сборщика 3 шурупа и 7 болтов. Сборщик взял один предмет, а затем другой. Найти вероятность того, что первый – шуруп, а второй – болт.
Решение. Пусть событие А ={первый шуруп}, тогда 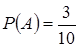
событие В ={второй болт}, тогда 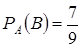 ,
,
а вероятность их одновременного появления 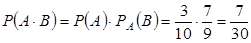 .
.
Пример. Найти вероятность появления слова АЛИБАБА, если каждая буква написана на отдельной карточке.
Решение. Пусть событие В={получилось слова АЛИБАБА}.
Событие В наступит, если первой буквой будет буква А (3 шанса из 7), второй буква Л (1 шанс из 6), третьей И (1 шанса из 5), четвертой – Б (2 шанс из 4), пятой – А (2 шанс из 3), шестой – Б (1 шанс из 1), шестой – А (1 шанс из 1).
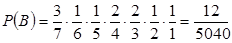
Формула полной вероятности. Формула Байеса
Следствием двух основных теорем – теоремы сложения и теоремы умножения вероятностей – является формула полной вероятности.
Теорема. Если событие F может произойти только при условии появления одного из событий (гипотез) 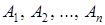 , образующих полную группу, то вероятность события F равна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующую условную вероятность события F.
, образующих полную группу, то вероятность события F равна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующую условную вероятность события F.
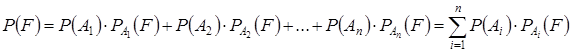 .
.
Пример. В магазине имеются микросхемы определенного вида, зная, что 1 поставщик завозит 70%, а второй – 30% всех микросхем и при этом 83% микросхем от 1 поставщика и 63% от 2-го работают без сбоев, найти вероятность покупки хорошей микросхемы.
Решение. Пусть событие F = {покупка хорошей микросхемы}, при условии, что 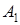 ={от 1 поставщика},
={от 1 поставщика}, 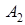 ={от 2 поставщика}, тогда согласно формуле полной вероятности имеем
={от 2 поставщика}, тогда согласно формуле полной вероятности имеем
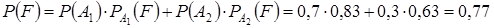 .
.
Формула Байеса.
Из теоремы умножения вероятностей и теоремы полной вероятности можно получит формулу переоценки вероятностей гипотез.
Она применяется, когда событие F, которое может появиться только с однойиз гипотез 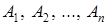 , образующих полную группу, ПРОИЗОШЛО и необходимо переоценить первоначальные (априорные) вероятности гипотез
, образующих полную группу, ПРОИЗОШЛО и необходимо переоценить первоначальные (априорные) вероятности гипотез 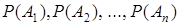 , то есть найти их апостериорные (опытные) вероятности
, то есть найти их апостериорные (опытные) вероятности 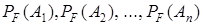 .
.
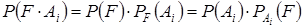 Þ
Þ 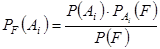 .
.
Заменим 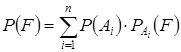 из формулы полной вероятности получим
из формулы полной вероятности получим
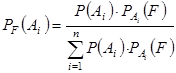 .
.
Пример. В торговую фирму поступили телевизоры от 3-х поставщиков в отношении 1:4:5. Практика показала, что телевизоры не требуют ремонта в течение срока гарантии соответственно в 98%, 88% и 92% случаях. Найти вероятность того, что поступивший в фирму телевизор не потребует ремонта, определить от кого он поступил?
Решение. а) Пусть событие 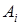 ={телевизор поступил от i поставщика} (i=1,2,3);
={телевизор поступил от i поставщика} (i=1,2,3);
F ={телевизор не потребует ремонта}.
Тогда,
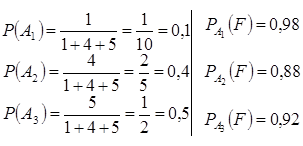
Тогда, из формулы полной вероятности
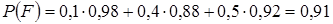 .
.
б) 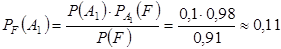 .
.
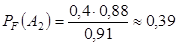 .
. 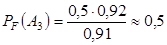 .
.
Как видим, после наступления события F вероятность гипотезы 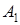 увеличилась,
увеличилась, 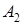 – уменьшилась,
– уменьшилась, 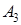 – осталось прежней.
– осталось прежней.
Данная схема называется схемой Бернулли.
Теорема. Если вероятность p наступления события А в каждом испытании постоянна, то вероятность 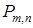 того, что событие А наступит m раз в n независимых испытаниях, равна
того, что событие А наступит m раз в n независимых испытаниях, равна
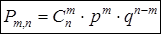 , где
, где 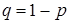
Задача. В среднем 20 % пакетов акций на аукционе продается по заявленной стоимости. Найти вероятность того, что из 9 пакетов в результате торгов по первоначальной цене:
1. не будут проданы 5 пакетов;
2. будут проданы:
а) менее двух пакетов;
б) хотя бы два пакета;
3. наивероятнейшее число пакетов.
1. Вероятность того, что пакет не будет продан по первоначальной цене
p=1–0,2=0,8
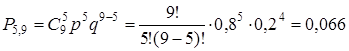
2. а. 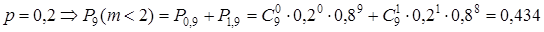
б. 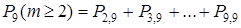
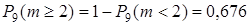
3. 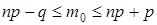 Þ
Þ 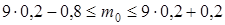 Þ
Þ 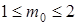
т.е. наивероятнейших чисел, в силу того, что границы есть числа целые, два.
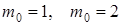
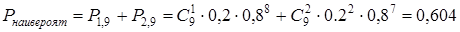
Задача. Тест содержит 10 вопросов, на которые следует отвечать да или нет. Какова вероятность получить не менее 80 % правильных ответов, используя метод угадывания.
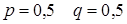
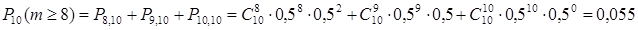
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|