Объяснение на конкретном примере темы по нахождению точек экстремума функции

Объяснение на конкретном примере темы по нахождению точек экстремума функции

Точки экстремума функции – это точки максимума и минимума функции, т.е. хmax, xmin – их обозначения

Например: дана функция у= ,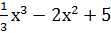

1) найдем производную этой функции и приравняем её к нулю:

;

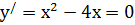2) решим полученное уравнение, корни х₁=0 и х₂=4 – это стационарные точки;

3) нанесём их на прямой луч:

+ - +

0 4

4) найдём знаки производной в каждом промежутке, подставляя любое число из промежутка в производную (в уме), смотрим знак (метод интервалов), (ну например беру число 10, подставляю в производную, получаю знак +, а т.к. это число из третьего интервала, то + туда и ставим, а далее чередуем), смотрите рисунок;

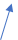5) вывод: если интервал содержит знак +, то функция на этом интервале возрастает ( ), а если знак минус, то функция убывает ( );

В нашем случае ответ: при х ? (-∞;0) и (4;+∞) функция возрастает;

При х ? (0;4) функция убывает;

6) хmax=0, т.к. к этой точке функция растёт, а после неё убывает (т.е. с + на -);

xmin=4, так как до этой точки функция убывала, а после неё возрастала (т.е. с – на +);

7) в 6-м пункте мы нашли точки экстремума, т.е. точки максимума и минимума, а теперь необходимо вычислить значения этих экстремумов, т.е. само максимальное значение и само минимальное значение функции; для этого точки макс и мин необходимо подставить в САМУ ФУНКЦИЮ, т.е.

У_max= ,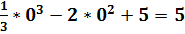

Уmin= .

Если необходимо вычислить ТОЧКИ ЭКСТРЕМУМА, то достаточно выполнить пункт 6), а если необходимо найти ЗНАЧЕНИЯ экстремумов, тогда и пункт 7.