- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Первообразная. Интеграл. четверть. четверть. четверть. четверть. Основные формулы планиметрии. Произвольный треугольник. Прямоугольный треугольник
Стр 1 из 2Следующая ⇒
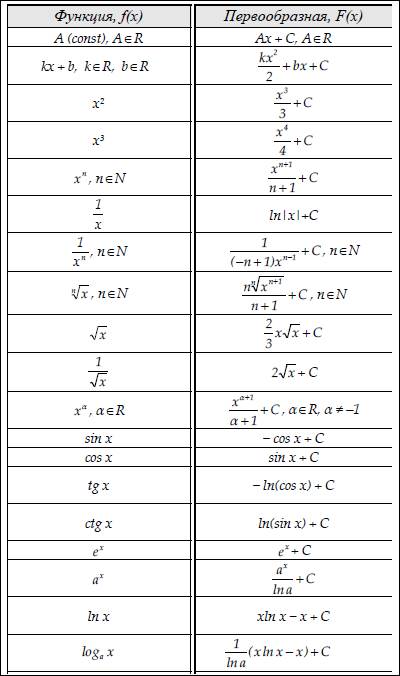
Первообразная. Интеграл
Функцию F(x) называют первообразной для функции f(x) на интервале (a; b), если на нем производная функции F(x) равна f(x):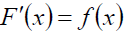 
Операцию, обратную дифференцированию называют интегрированием.
Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен площади криволинейной трапеции, образованной линиями: сверху ограниченной кривой у = f(x), и прямыми у = 0; х = a; х = b.
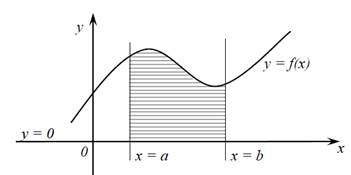
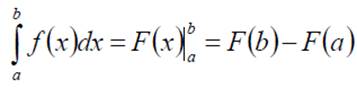
S =
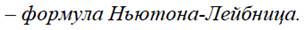
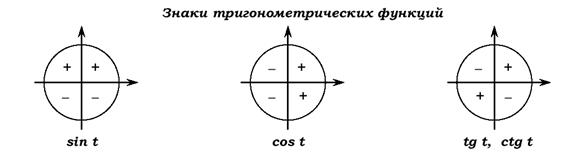
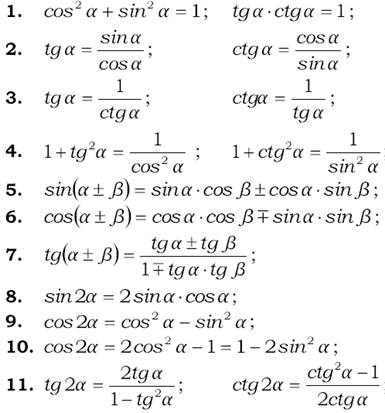Значения тригонометрических функций.
1 четверть
2 четверть
3 четверть
4 четверть
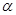
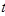
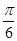
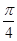
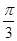
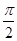
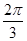
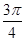
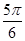
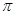
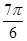
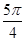
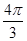
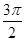
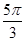
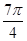
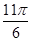
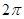
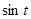
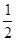
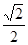
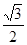
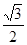
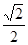
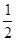
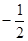
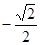
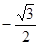
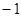
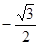
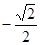
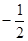
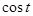
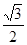
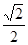
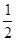
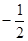
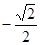
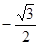
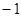
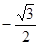
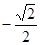
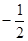
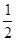
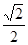
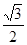
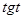
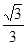
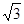
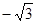
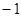
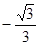
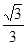
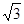
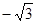
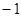
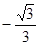
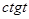
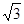
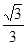
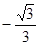
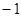
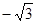
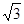
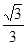
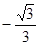
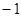
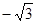
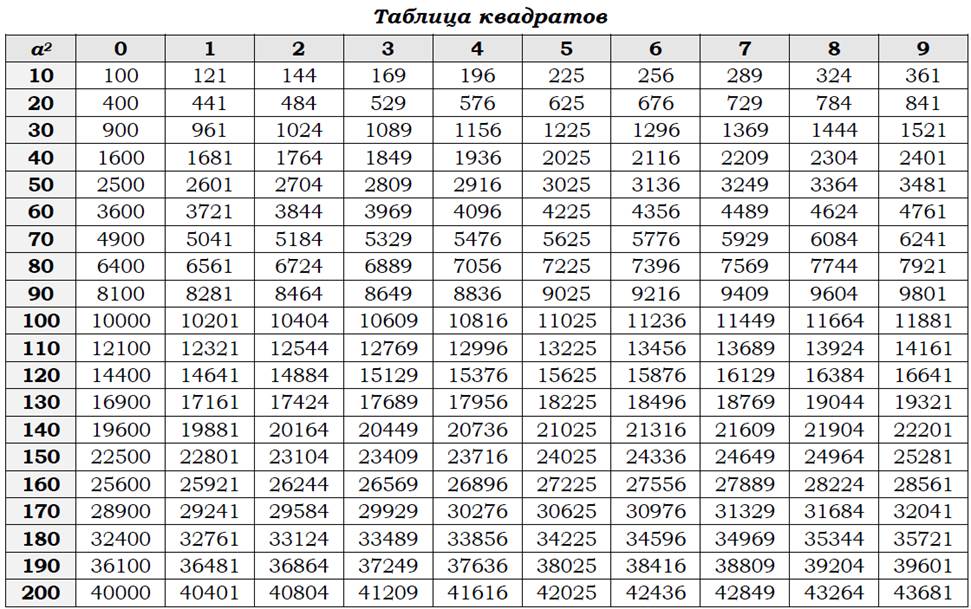
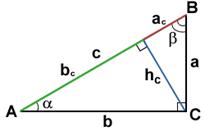Площадь
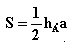
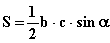
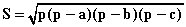
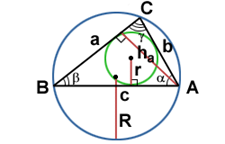
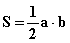Теорема SIN
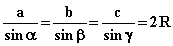
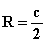Радиус вписанной окружности
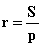
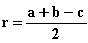Радиус описанной окружности
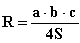
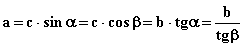
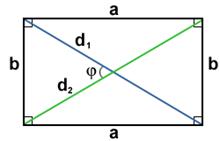
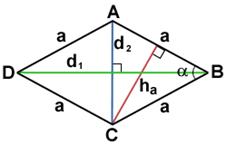a и b - смежные стороны
a - угол между ними
ha - высота, проведенная к стороне a
d1 и d2 - диагонали
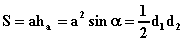Площадь
