процедура перевода сырых оценок в стеновую шкалу. Есть 2 способа.

Стандартизация данных.

процедура перевода сырых оценок в стеновую шкалу. Есть 2 способа.

Все возможные виды нормального распределения отличаются друг от друга только 2 параметрами:

- среднее арифметическое

- стандартное отклонение

Нам известны эти два параметра для стеновой шкалы: среднее арифметическое = 5,5, стандартное отклонение = 2.

Чтобы перевести наши сырые оценки (распределение которых соответствует нормальному закону) в стеновую шкалу нужно найти среднее арифметическое и ст. отклонение в нашем эмпирическом распределении. Это среднее арифметическое будет соответствовать 5,5 на стеновой шкале. То есть наше рассчитанное стандартное отклонение для нашей выборки как бы будет равно 5,5 стенам.

И далее возможно два способа перевода, в зависимости от того, как мы определяем эту точку 5,5 на стеновой шкале.

Дело в том, что стеновая шкала - интервальная. Например, 1 стен - это диапазон значений, который мы условно обозначим 1. И точка 5,5 - она условная, ее на самом деле не существует.

1 способ(лучше расчеты делать по этому способу, т. к. на других занятиях от вас будут требовать перевод именно так):

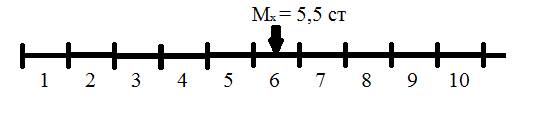
На нашей стеновой шкале мы отсчитываем 5 интервалов и еще половинку интервала. Условная точка 5,5 будет приходиться на середину 6-ого интервала. Теперь наша задача состоит в том, чтобы определить границы интервалов, а вернее, какие значения сырых оценок будут соответствовать этим границам (точкам, отделяющим один стен от другого). Поскольку известная нам точка находится в середине 6-ого интервала, то начинаем с него.

Так как стандартное отклонение в стеновой шкале = 2ст, то один стен (один интервал) равен половине стандартного отклонения. Соответственно точка 5,5 находится на расстоянии +1/4 стандартного отклонения от границ 6-ого интервала стеновой шкалы. Берем рассчитанное среднее арифметическое для нашего эмпирического распределения, отнимаем от него 1/4 эмпирического стандартного отклонения, получаем точку, соответствующую границе между 5 и 6 стенами. Прибавляем 1/4 ст. отклонения к среднему арифметическому - получаем точку, соответствующую границе между 6 и 7 стенами. Для расчета следующих границ интервалов нужно отнимать/прибавлять уже по 1/2 ст. отклонения. Так, границе между 4 и 5 стенами будет соответствовать точка: сред арифметическое - 1/4 ст. отклонения - 1/2 ст. отклонения

И т. д.

Результатом работы должен стать рисунок с обозначениями границ интервалов в сырых баллах или таблица вида:

1 стен	2 стена	3 стена	4 стена	5 стенов	6 стенов	7 стенов	8 стенов	9 стенов	10 стенов
<5	6-9	10-12	13-17	18-22	23-31	32-38	39-44	45-50	>50

*диапазоны значений, соответствующие каждому из стенов, даны произвольно, только как иллюстрация

2 способ.

Поскольку стеновая шкала - интервальная, то перевод ее в шкалу отношений осуществляется путем нахождения середины интервалов. Например, число 3 будет соответствовать середине 3 его интервала, 4 - середине 4ого и т д. Справа и слева от этих точек будет находится по 0,5 интервала (стена). Так, границы интервала 5 будут соответствовать значениям 4,5 и 5,5 на шкале отношений. И среднее арифметическое стеновой шкалы 5,5 будет приходиться на границу между интервалами 5 и 6. Чтобы рассчитать следующие границы, нужно отнимать/прибавлять по 1/2 ст. отклонения от нашего эмпирического среднего арифметического.

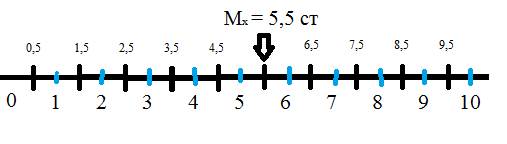
Разница между 1 и 2 способами расчетов заключается в том, что при втором способе получается 11 интервалов в стеновой шкале, где первый нулевой интервал - от минус бесконечности до 0,5, а последний 10й - от 9,5 до плюс бесконечности.

При первом способе расчета интервалов всего 10, нулевого интервала нет.