Практическая работа 17. Обратные тригонометрические функции: арксинус, арккосинус, арктангенс. вариант. вариант. Теоретические положения

Практическая работа 17

Обратные тригонометрические функции: арксинус, арккосинус, арктангенс

Цель работы: Обобщить и систематизировать знания по теме «Обратные тригонометрические функции. Арксинус, арккосинус, арктангенс»; закрепить умения использовать полученные знания для преобразования тригонометрических выражений.

Дидактический материал для выполнения практической работы:

Методические рекомендации для выполнения практических работ, тетрадь для практических работ, конспект лекций.

Задания:

1 вариант

Вычислите:

а) ;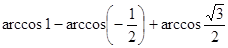

б) ;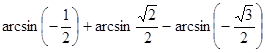

в) 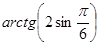; г) ;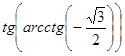

д) ;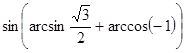

е) .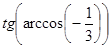

2 вариант

Вычислите:

а) ;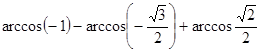

б) ;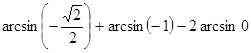

в) 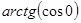; г) ;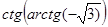

д) ;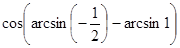

е) .

Требования к отчету:

Отчет должен содержать решение заданий с указаниями на теоретические факты, использованные при решении.

Теоретические положения

Для того чтобы ввести именно обратную функцию к возведению в квадрат и было предложено понятие арифметического квадратного корня, который дает только неотрицательные значения. Т.е. для функции 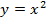обратной функцией считается .

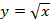Аналогично существуют и функции, обратные к тригонометрическим, их называют обратными тригонометрическими функциями. К каждой из рассмотренных нами функций существует своя обратная, их называют: арксинус, арккосинус, арктангенс и арккотангенс.

Эти функции решают задачу вычисления углов по известному значению тригонометрической функции. Например, с использованием таблицы значений основных тригонометрических функций можно вычислить синус какого угла равен 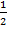. Находим это значение в строке синусов и определяем, какому углу оно соответствует. Первое, что хочется ответить, что это угол 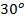или , но если у вас в распоряжении таблица значений до 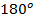, вы тут же заметите еще одного претендента на ответ, - это угол 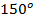или 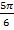. А если мы вспомним о периоде синуса, то поймем, что углов, при которых синус равен 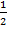, бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для косинусов, тангенсов и котангенсов, т.к. все они обладают периодичностью.

Т.е. мы сталкиваемся с той же проблемой, которая была для вычисления значения аргумента по значению функции для действия возведения в квадрат. И в данном случае для обратных тригонометрических функций было введено ограничение области значений, которые они дают при вычислении. Это свойство таких обратных функций называют сужением области значений, и оно необходимо для того, чтобы их можно было называть функциями.

Для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно. Например, арксинус возвращает значения углов в диапазоне от 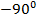до .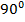

Критерии оценки

Все этапы заданий выполнены верно, логически грамотно, нет неточностей – оценка 5; оценка 4 ставится, если была допущена неточность или не указана аксиома или ее следствие, которые использованы при решении задач; если была допущена серьезная ошибка, повлекшая неверный ответ, то ставится оценка 3, во всех остальных случаях ставится оценка 2.