Метод нулевых моментных точек

Метод нулевых моментных точек

Использование метода нулевых моментных точек позволяет значительно упростить решение ряда задач строительной механики, связанных с расчетом статически неопределимых конструкций. Суть метода нулевых моментных точек рассмотрим на примере однопролетной балки с жестким защемлением на одной их опор.

Однопролетная балка с жестким защемлением на опоре А и шарнирными связями на опоре В является один раз статически неопределимой. Если мы приложим на опоре В некоторый изгибающий момент, то на опоре А - жестком защемлении - возникнет реактивный опорный момент, который будет в 2 раза меньше приложенного на опоре В момента и будет иметь противоположный знак. Соответственно, если построить эпюру моментов для такой балки (см. рисунок 504.1 а)), то на расстоянии 2/3 от точки В будет нулевая моментная точка (или точка, в которой момент меняет знак). Таким образом, и с точки зрения значения моментов и с точки зрения значения поперечных сил однопролетная один раз статически неопределимая балка длиной l с жестким защемлением на опоре А и шарнирными связями на опоре В соответствует однопролетной статически определимой балке с шарнирными связями на обеих опорах, но имеющей длину 2l/3.

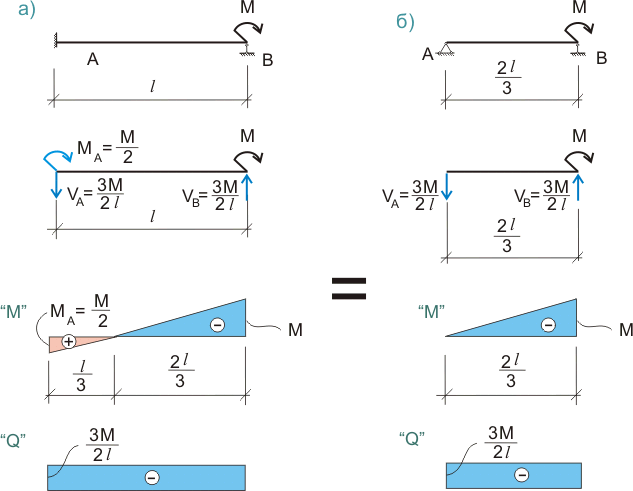Рисунок 504.1. Примечание: Так как больше никаких нагрузок на рассматриваемые балки не действует, то поперечные силы (касательные напряжения) действующие в нулевой моментной точке балки с жестким защемлением на одной из опор, равны опорной реакции для эквивалентной ей балки с двумя шарнирными опорами. Таким образом при выполнении некоторых видов расчетов один раз статически неопределимую балку с жестким защемлением на одной из опор можно заменять на эквивалентную ей статически определимую балку, имеющую длину 2l/3. Этот же метод применим и в тех случаях, когда на рассматриваемую балку действуют одинаковые по значению и направлению моменты приложенные на концах балки. В этом случае нулевая моментная точка будет посредине и соответственно эквивалентная балка будет иметь длину l/2.