Контрольная работа по теории чисел

Контрольная работа по теории чисел

для студентов группы ФМФИ-б18МФз 2020/21 учебный год

ФИО студента	Вариант контрольной работы	Вариант теста
Аношина Анастасия Дмитриевна
Афимьина Наталья Георгиевна
Афонасьева Влада Владимировна
Вавилина Ольга Владимировна
Власов Алексей Олегович
Горбаченко Дарья Петровна
Кобрицова Алла Андреевна
Коротких Оксана Игорьевна
Магомедова Луиза Магомедовна*
Тяжова Надежда Владимировна
Филиппов Владислав Александрович
Шмургалкина Татьяна Александровна*
Зубкова Оксана Павловна

Максимальная оценка за задачи контрольной работы

задача

всего

баллы

За каждое здание в тесте оценка о или 1 балл.

Экзамен по расписанию 26.04.2021.

Контрольная работа и тест должны быть сданы до 26.04.2021 г.

Вариант 1

1. Докажите, что при любом целом n выражение 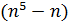делится на 5.

2. Найдите НОД и НОК чисел 1232 и 1672 (двумя способами).

3. Вычислите 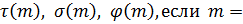1377.

4. Решите уравнение в целых числах 237х+44у=1

5. Найдите две последние цифры числа .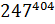

6. Решите сравнение методом Эйлера .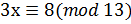

7. Решите сравнение с помощью непрерывных дробей .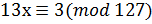

8. Решите сравнение любым методом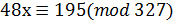

9. Найдите показатель числа а=7 по модулю m=13. Является ли число 7 первообразным корнем по модулю 13?

10. Докажите, что ни для одного многочлена f(x) с целыми коэффициентами не могут иметь место равенства f(7)=11 и f(11)=13.

11. Докажите, что частные от деления двух чисел на их наибольший общий делитель есть числа взаимно простые.

Вариант 2

1. Докажите, что при любом натуральном n число ( 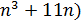делится на 6.

2. Найдите НОД и НОК чисел 9900 и 72765 (двумя способами)

3. Вычислите 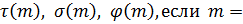1134.

4. Решите уравнение в целых числах 26х-31у=35.

5. Найдите остаток от деления 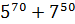на 12.

6. Решите сравнение методом Эйлера .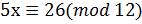

7. Решите сравнение с помощью непрерывных дробей .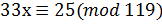

8. Решите сравнение любым методом .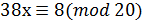

9. Найдите число первообразных корней и наименьший из них по модулю р=29.

10. Докажите, что числа р и 8р²+1 могут быть одновременно простыми только при р=3.

11. Докажите, что сравнения по одному модулю можно почленно складывать.

Вариант 3

1. Докажите, что произведение четырех последовательных целых чисел делится на 12.

2. Найдите НОД и НОК чисел 549 и 387 (двумя способами)

3. Вычислите 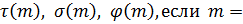1365.

4. Решите уравнение в целых числах 31х+42у=17.

5. Найдите две последние цифры числа .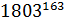

6. Решите сравнение методом Эйлера .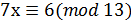

7. Решите сравнение с помощью непрерывных дробей .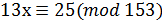

8. Решите сравнение любым методом .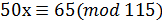

9. Найдите показатель числа а= 3 по модулю m= 25. Является ли число 3 первообразным корнем по модулю 25?

10. Найдите все пары натуральных чисел (x, y) таких, что x+y=150 и НОД(x, y)=30.

11. Докажите, что сравнения по одному модулю можно почленно умножать.

Вариант 4

1. Докажите, что если число не делится на 5, то его квадрат, увеличенный или уменьшенный на 1, делится на 5.

2. Найдите НОД и НОК чисел 1287 и 765 (двумя способами)

3. Вычислите 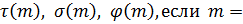4081.

4. Решите уравнение в целых числах 47х+17у=10.

5. Найдите остаток от деления 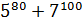на 17.

6. Решите сравнение методом Эйлера .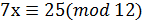

7. Решите сравнение с помощью непрерывных дробей .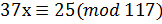

8. Решите сравнение любым методом .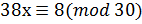

9. Найдите число первообразных корней и наименьший из них по модулю р=17.

10. Докажите, что если х и у – целые числа такие, что 3х+8у делится на 17, то число 35х+65у также делится на 17.

11. Докажите, что обе части сравнения и модуль можно разделить на одно и тоже натуральное число.

Вариант 5

1. Докажите, что при любом целом n выражение n²(n²-1) делится на 6

2. Найдите НОД и НОК чисел 1014 и 6120 (двумя способами)

3. Вычислите 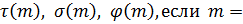2268.

4. Решите уравнение в целых числах 127х+177у=67.

5. Найдите две последние цифры числа .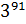

6. Решите сравнение методом Эйлера .

7. Решите сравнение с помощью непрерывных дробей .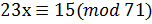

8. Решите сравнение любым методом .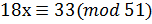

9. Найдите число первообразных корней и наименьший из них по модулю р=31

10. Найдите значения простого р, если известно, что р+10 и р+14 – тоже простые числа.

11. Докажите, что если 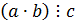и (a, c)=1, то .

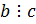Вариант 6

1. Докажите, что при любом целом n выражение n²(n²-1) делится на 12.

2. Найдите НОД и НОК чисел 988 и 6292 (двумя способами)

3. Вычислите 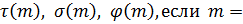2475.

4. Решите уравнение в целых числах 28х-19у=7

5. Найдите остаток от деления 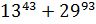на 18

6. Решите сравнение методом Эйлера .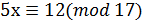

7. Решите сравнение с помощью непрерывных дробей ..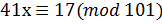

8. Решите сравнение любым методом .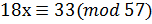

9. Найти показатель числа а=5 по модулю m=29. Является ли число 5 первообразным корнем по модулю 29?

10. Найдите наименьшее натуральное число вида 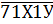, делящееся на 45

11.Докажите, что множество простых чисел бесконечно.

Вариант 7

1. Докажите, что произведение четырех последовательных целых чисел делится на 24.

2. Найдите НОД и НОК чисел 2964 и 6292 (двумя способами)

3. Вычислите 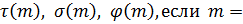27144.

4. Решите уравнение в целых числах 7х - 12у = 15.

5. Найдите две последние цифры числа .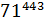

6. Решите сравнение методом Эйлера .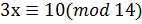

7. Решите сравнение с помощью непрерывных дробей ..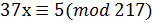

8. Решите сравнение любым методом .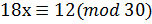

9. Найти показатель числа а=7 по модулю m=17. Является ли число 7 первообразным корнем по модулю 17?

10. Найдите наименьшее натуральное число вида 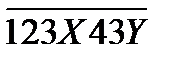, делящееся на 9.

11.Докажите, что если а ∶ с и b ∶ с, то (а + b) ∶ с .

Тесты

Вариант 1

№ 1. Если a делится на c, b не делится на c, то:

1) a+b делится на c; 2) a+b не делится на c;

3) a+b может делится на c, а может не делится на c; 4) a-b делится на c.

№ 2. Если d - наибольший общий делитель чисел a и b, то:

1) на d делится любой общий делитель чисел a и b;

2) d делится на любой общий делитель чисел a и b;

3) d делится на a и b;

4) a делится на d и b не делится на d.

№ 3. Если числа a и b взаимно простые, то не имеет решения в целых числах уравнение:

1) 2ax+2by =1; 2) ax+by =-1; 3) ax+by =1; 4) ax-by =1.

№ 4. Сравнение 16x≡20 (mod 28) имеет:

1) одно решение; 2) четыре решения; 3) не имеет решений;

4) имеет два решения.

№ 5. По модулю 8 полной системой вычетов является:

1) {-3, -5, 0, 3, 5};

2) {0, 9, -2, 6, 2, 5, 7, 8};

3) {-1, 0, 2, 4, 5, 9, 11, 14};

4) {4, 2, 11, 12, 13}.

№ 6. a=2⁵∙3²∙7∙11³; b=2³∙5²∙7²∙13. Наибольший общий делитель этих чисел равен: _____________ .

№7. Расположите числа в порядке возрастания остатков от деления на 5:

83, 22, -30, 44, -24.

№8. Расположите цепные (непрерывные) дроби в порядке возрастания равных им чисел:

(0; 1, 2, 5); (0; 2, 1, 4); (0; 1, 7, 8); (1; 2, 9, 3).

№9. Расположите пары чисел в порядке возрастания их НОД:

12 и 18; 15 и 21; 16 и 20; 12 и 13.

№10. Наименьший отличный от единицы делитель составного числа а:

1) Не превосходит 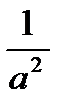; 3) Не превосходит ;

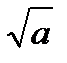2) Превосходит 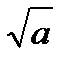; 4) Превосходит а+2.

№ 11. На 15 делится число:

1) 212784532127845; 3) 127845127845127845;

2) 32127845332127845; 4) 4100255.

Вариант 2

№ 1. Если a делится на d, то ab делится на d при:

1) любом целом b; 2) при положительном действительном b;

3) при отрицательном рациональном b; 4) только при b=3.

№ 2. Если m-наименьшее общее кратное чисел a и b, то:

1) на m делится число a;

2) на m делится любое общее кратное чисел a и b;

3) m делится на любое общее кратное чисел a и b;

4) на m делится число b.

№ 3. Если числа a и b взаимно простые, то:

1) НОК[a, b]=a; 2) НОК[a, b]=a∙b; 3) НОК[a, b]=b; 4) НОК[a, b]=1.

№ 4. Сравнение 15x≡20 (mod 14) имеет:

1) имеет два решения; 3) не имеет решений;

2) имеет пять решений; 4) имеет одно решение.

№ 5. Приведенной системой вычетов по модулю 12 будет:

1) {-5, 13, 11, -21, 5};

2) {7, 25, 11, -21, 17};

3) {4, 15, 7, 11, 19};

4) {1, 5, 7, 11}.

№ 6. a=2⁵∙3²∙7∙11³; b=2³∙5²∙7²∙13. Наименьшее общее кратное этих чисел равно:

1) m=2³∙7²∙11∙13; 2) m=2⁵∙3²∙5²∙7²∙11³∙13; 3) m=2⁵∙7²; 4) m=2⁸∙3²∙7.

№7. Расположите числа в порядке возрастания остатков от деления на 6:

123, -36, 68, -20, 35, 25.

№8. Расположите цепные (непрерывные) дроби в порядке убывания равных им чисел:

(0; 1, 2, 5), (0; 2, 1, 4), (0; 1, 7, 8), (1; 2, 9, 3).

№9. Наименьшее общее кратное трех чисел равно их произведению, если они:

1) Все четные ; 2) Все нечетные; 3) Попарно взаимно простые;

4) Одно число четное, а другие - нечетные

№ 10. На 15 делится число:

1) 213684532127845; 2)127845127845127845;

3) 32127845332127845; 4)4100255.

№11. Произведение любых трех последовательных натуральных чисел делится на:

1) 2 и 7; 2) 3 и 5; 3) 2 и 3; 4) 2 и 5