
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Введение нового способа решения тригонометрических уравнений.
Введение нового способа решения тригонометрических уравнений.
Познакомимся с решением тригонометрических уравнений новым способом: с помощью замены одной из тригонометрических функций и сведением к квадратному уравнению.
| Вид уравнения | Подходящая замена | |
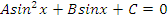
| 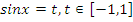
| |
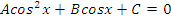
| 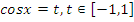
| |
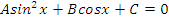
| 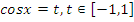
| |
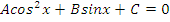
| 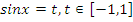
| |
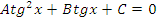
| 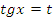
| |
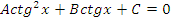
| 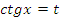
| |
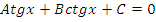
| 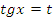 или или 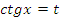
|
Разберем несколько примеров:
1) 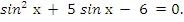
Данное уравнение соответствует (1) таблицы, поэтому делаем замену 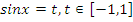 ,
,
- получаем квадратное уравнение:
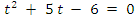 ,
, - находим корни
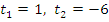 ,
, - замечаем, что
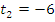 посторонний корень, поскольку
посторонний корень, поскольку 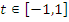 ,
, - делаем обратную замену, т.е. решаем уравнение
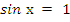 , у которого корнями будут числа
, у которого корнями будут числа 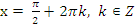 .
.
Ответ: 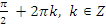 .
.
2) 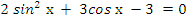 .
.
Данное уравнение соответствует (3) таблицы, поэтому cделаем замену 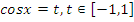 . Из основного тригонометрического тождества следует, что
. Из основного тригонометрического тождества следует, что 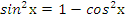 ,
, 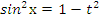 ,
,
- получим квадратное уравнение:
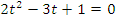 ,
, - находим корни:
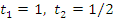 ,
, - делаем обратную замену:
-
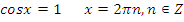 или
или -
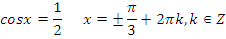
Ответ: 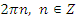 ,
, 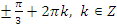 .
.
3) 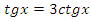 .
.
Данное уравнение соответствует (7) таблицы, поэтому можно сделать замену 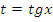 или
или 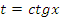 . После решения примера самостоятельно сделайте другую замену и сравните ответы.
. После решения примера самостоятельно сделайте другую замену и сравните ответы.
Сделаем, например, замену 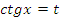 , вспомним, что
, вспомним, что 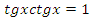 , поэтому
, поэтому 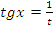 , получим уравнение
, получим уравнение 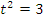 , откуда
, откуда 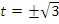 или, делая обратную замену,
или, делая обратную замену, 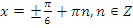 .
.
Ответ: 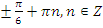 .
.
4) 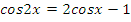 .
.
Данное уравнение непосредственно не имеет вид, описанный в таблице. Как правило, легко классифицировать уравнения, если привести тригонометрические функции в него входящие к одному аргументу. Поскольку 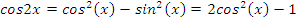 , то уравнение сведено к (2) виду таблицы. Поэтому делаем замену
, то уравнение сведено к (2) виду таблицы. Поэтому делаем замену 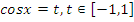 и получаем неполное квадратное уравнение
и получаем неполное квадратное уравнение 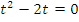 , откуда
, откуда 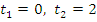 . (
. ( 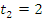 посторонний корень, поскольку
посторонний корень, поскольку 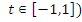 .
.
Делаем обратную замену:
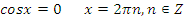
Ответ: 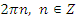 .
.
Выберите одно из предложенных уравнений и самостоятельно решите его.
| На оценку | 1 вариант | |
| задание | ответ | |
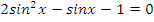
| 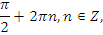
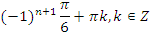
| |
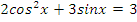
| 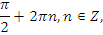
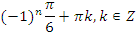
| |
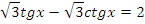
| 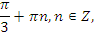

| |
| 2 вариант | ||
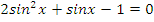
| 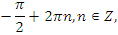
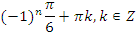
| |
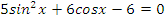
| 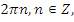
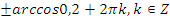
| |
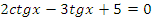
| 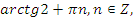
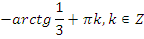
| |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|