Температурные эффекты

2.5. Температурные эффекты

Предположим, что исследуемое тело находится в неоднородном и нестационарном температурном поле Т(х_i, t). Температура отсчитывается от некоторого начального значения T₀. Согласно гипотезе Неймана полная линейная деформация складывается из деформаций от силовой нагрузки 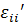и температурного расширения 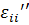= 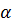Т:

Т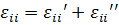емпературные добавки для сдвиговых деформаций равны нулю. Поэтому закон Гука с учетом температуры принимает вид

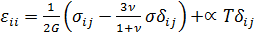. (2.15)

Величину называют коэффициентом линейного температурного расширения материала. Выражая напряжения через деформации из (2.15), получаем

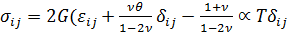Соотношение между девиаторами в термоупругости остается тем же, что и в случае идеальной упругости (2.9), иную форму принимает только связь шаровых частей тензоров напряжений и деформаций

, .

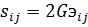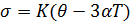Компоненты деформаций в (2.15) связаны с перемещениями соотношениями Коши (1.25).

В сложных задачах термоупругости в общем случае предварительно нужно решить также задачу о распределении тепла. Температура T(x_i, t) в каждой точке тела должна удовлетворять уравнению теплопроводности

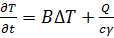, (2.16)

где В — температуропроводность материала; — оператор Лапласа

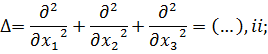
Q(x_i, t) — функция, показывающая количество тепла, которое производится источником тепловой энергии в единице объема и за единицу времени; с — удельная теплоемкость; — удельный вес.

К уравнению (2.16) следует добавить начальные условия распределения температуры Т(x_i, 0) = f(xi). Кроме этого на границе твердого тела должны выполняться условия теплообмена с окружающей средой (три типа условий теплообмена [29]).

При достаточно высоких температурах нельзя пренебрегать зависимостью констант упругости от температуры. Для ее описания можно использовать формулу Белла [5], предложенную им после экспериментального исследования более 500 металлов и сплавов,

{G(T), Е(Т), К(Т)} = {G(0), Е(0), К(0)} 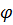(Т).

Здесь G(T), Е(Т), К(Т) —модули упругости при температуре T (в градусах Кельвина); 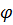(Т) —линейная функция температуры,

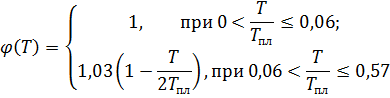
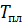— температура плавления материала; G(0), Е(0), К(0)—значения параметров упругости при так называемом нулевом напряжении. Эти значения легко получить, если знать величину одного из модулей упругости при некоторой, например комнатной, температуре и температуру плавления материала. В частности, для сплава Д16Т

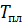= 933 К, G(0) = 0,308 • 10⁵ МПа, E(0) = 0,829 • 10⁵ МПа.

Вообще говоря, величина Q в (2.16) для деформируемых тел зависит от напряженного и деформированного состояний. В этом случае говорят о связанных задачах термоупругости.

Для анизотропного упругого тела закон Гука (2.11) примет вид

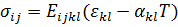Здесь 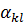— тензор коэффициентов термического расширения материала. Постоянные 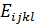определяются в изотермических условиях при Т = T₀. Если приращение температуры не мало, то 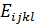и 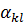должны рассматриваться как функции температуры.

12 Следующая ⇒