Алгебра. 8 класс. Тема урока: Контрольно-обобщающий урок по теме «Неравенства». КЛАССНАЯ РАБОТА. Числовые неравенства и их свойства. Сложение и умножение неравенств, возведение в степень. Решение неравенств с одной переменной. В результате следующих прео

22.04.2020 .

Алгебра. 8 класс

Тема урока: Контрольно-обобщающий урок по теме «Неравенства»

Цели: -развивать навыки рефлексии, самоанализа и критического мышления;

-обобщить и систематизировать знания по теме «Неравенства»

КЛАССНАЯ РАБОТА

1.Давайте повторим теорию решения неравенств и систем неравенств.

Числовые неравенства и их свойства

Определение

Число a больше числа b, если разность a – b – положительное число.

Число a меньше числа b, если разность a – b – отрицательное число.

Если разность равна 0, то числа a и b равны.

Свойства

1. Если a > b, то b < a; если a < b, то b > a.

2. Если a < b и b < c, то a < c.

3. Если a < b и c – любое число, то a + c < b + c.

4. Если a < b и c – положительное число, то ac < bc;

если a < b и c – отрицательное число, то ac > bc.

5. Если a и b – положительные числа и a < b, то .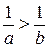

Сложение и умножение неравенств, возведение в степень

6. Если a < b и c < d, то a + c < b + d.

7. Если a, b, c и d – положительные числа, a < b и c < d, то ac < bd.

8. Если a и b – положительные числа, n – натуральное число и a < b, то aⁿ < bⁿ.

Решение неравенств с одной переменной

Определения

Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.

Решить неравенство – значит найти все его решения или доказать, что решений нет, то есть найти множество решений неравенства.

В результате следующих преобразований

получается неравенство, равносильное данному:

1) Если из одной части неравенства перенести в другую слагаемое, изменив знак этого слагаемого на противоположный.

2) Если обе части неравенства умножить или разделить на одно и то же положительное число.

3) Если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.

Определение

Неравенства вида ax < b, ax > b, ax ≤ b, ax ≥ b, где a и b – некоторые числа, называются линейными неравенствами.