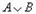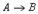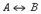Хелпикс

Главная

Контакты

Случайная статья



Опр.4 Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение.

⇐ ПредыдущаяСтр 3 из 3


Опр.4 Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение.

Посылками умозаключения по правилам формальной логики могут быть только истинные суждения. Тогда, если умозаключение проводится в соответствии с правилами формальной логики, то оно будет истинным. В противном случае можно прийти к ложному умозаключению.

Например:

1. Все металлы – простые вещества. Литий – металл. Литий – простое вещество. 2. Все школьники – отличники. Вовочка – школьник. Вовочка – отличник.

Опр.7 Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.

Рассмотрим три базовых логических операций – инверсию, конъюнкцию, дизъюнкцию и дополнительные – импликацию и эквивалентность.

 


Логическая операция Название Соответствует союзу Обозначениезнаками Таблица истинности Логическая операция
Инверсия (от лат. inversion – переворачиваю) отрицание не А
А
Опр. 8 Инверсия логической переменной истина, если переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
Конъюнкция (от лат. conjunction – связываю) Логическое умножение А и В
А В
Опр.9Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания, истинны.
Дизъюнкция (от лат. disjunction – различаю) Логическое сложение А или В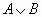
А В
Опр. 10 Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны.
Импликация (от лат. implication – тесно связывать) Логическое следование Если А, то В; Когда А, тогда В 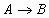А–условие В-следствие
А В
Опр. 11 Импликация двух логических переменных ложна тогда и только тогда, когда из истинного основания следует ложное следствие.
Эквивалентность(от лат. equivalents - равноценность) Логическое равенство А тогда и только тогда, когда В
А В
Опр. 12 Эквивалентность двух логических переменных истинна тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны

 

Д.З.

1. Выучить основные законы логики.

2. Придумать по два примера на каждый закон логики.

3. Найти в Интернет информацию об основных законах логики.

 


⇐ Предыдущая123
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.