Контакты

Случайная статья

Дробно-рациональные уравнения, сводящиеся к квадратным.

Дробно-рациональные уравнения, сводящиеся к квадратным.

1. Решить уравнение:

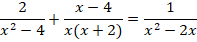Выпишем условие (*)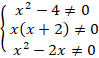

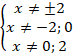
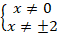
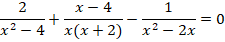
Разложим знаменатели на множители:

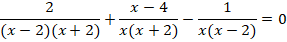
Приведем все дроби к общему знаменателю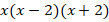

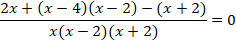
Дробь равна 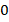, если ее числитель равен :

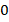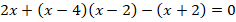
Раскрыв скобки и приведя подобные слагаемые, получаем квадратное уравнение:

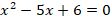
Найдем корни квадратного уравнения:

Х1=2, х2=3

Корень 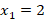не удовлетворяет условие (*)

Ответ: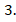

2. Решить уравнение:

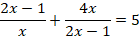
Выпишем условие (*)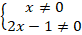

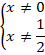
Обратим внимание, что неизвестная 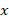присутствует в уравнении в похожих конструкциях

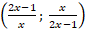они являются взимнообратными выражениями. В таком случае можно применить метод замены переменной:

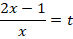
Тогда:

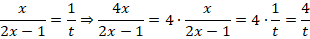
Исходное уравнение будет иметь вид:

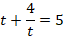
Чтобы избавиться от дроби, умножим обе части уравнения на 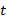, при этом 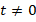, поскольку :

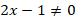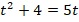
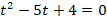
Получили квадратное уравнение, решениями которого являются:

t = 1, t = 4

Вернемся к замене:

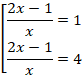
Решаем первое уравнение:

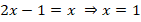
Решаем второе уравнение:

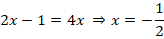
Полученные корни удовлетворяют удовлетворяют (*). Ответ: .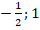

3. Решить уравнение:

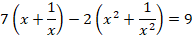
Решение.

Выпишем условие (*)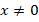

В подобных уравнениях стандартной является замена:

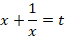
Чтобы выразить 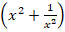через 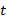, произведем следующие действия:

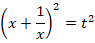
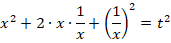
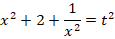
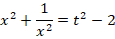
После замены исходное уравнение будет иметь вид:

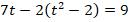
Преобразуя это выражение, получаем квадратное уравнение:

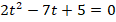
Найдем корни уравнения:

t = 2,5; t = 1

Вернемся к замене:

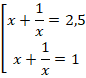
Поскольку 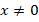, можем умножить обе части каждого из уравнений на 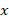и получить квадратные уравнения:

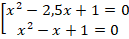
Первое уравнение имеет решения:

x = 2; x = 0,5

Оба решения удовлетворяют условие (*).

Второе уравнение не имеет корней.

Ответ: .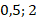

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.