Объяснение нового материала

Занятие по теме: « Бином Ньютона. Треугольник Паскаля».

Цель занятия: Познакомить с биномом Ньютона, показать его связь с треугольником Паскаля.

План занятия: 1. Повторение формул сокращенного умножения.

2. Новый материал.

3. Закрепление нового материала.

4. Домашнее задание.

1. Повторение.

2. Объяснение нового материала

Формулы сокращённого умножения являются частным случаем бинома Ньютона.

Как возвести в степень n сумму двух слагаемых? Формула бинома Ньютона относится к алгебре, к ветви математики, называемой комбинаторикой!
Многочлен это Полином - другими словами - сумма произвольного числа слагаемых называется полином. А сумма двух слагаемых называется Бином!

Рассмотрим целые неотрицательные степени бинома (а+в):

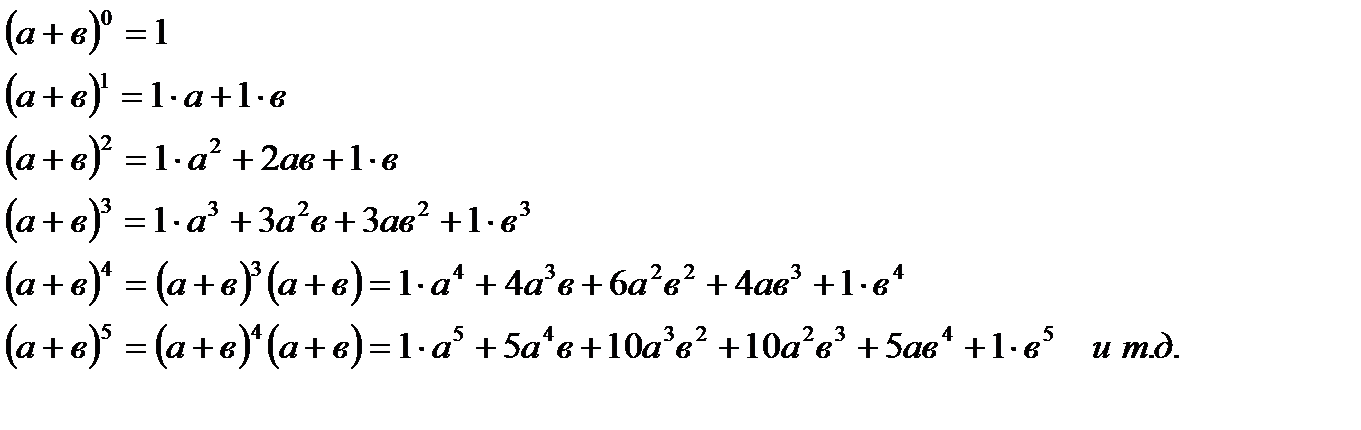
Ньютон изобрел формулу, которая позволяет возвести сумму двух слагаемых в степень с любым показателем, а не только с показателем равным 2!

Эта формула называется биноминальной формулой Ньютона или просто бином Ньютона:

Биноминальные коэффициенты легко находить с помощью так называемого треугольника Паскаля.

Поскольку числа, составляющие треугольник Паскаля, являются биномиальными коэффициентами, то треугольник Паскаля можно переписать в другом виде:

4. Закрепление.

Учитывая всё замеченное очень просто записать степень двучлена с любым натуральным показателем.

Запишем (а + в)⁵ = _______________________________________

Коэффициенты слагаемых Показатель степени Полученные слагаемые

1 слагаемое 1 2 слагаемое 5 3 слагаемое 10 4 слагаемое 10 5 слагаемое 5 6 слагаемое 1 а⁵в⁰ а⁴в¹ а³в² а²в³ а¹в⁴ а⁰в⁵ 1а⁵в⁰ 5а⁴в¹ 10а³в² 10а²в³ 5а¹в⁴ 1в⁵

Таким образом, получаем:

(а + в)⁵ = а⁵ + 5а⁴в + 10а³в² + 10а²в³ + 5ав⁴ + в⁵ .

Или ещё такая задача которую можно решить с помощью треугольника Паскаля.

Или по формуле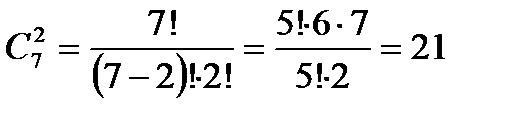

Пример 3. Записать разложение бинома

Домашнее задание: написать конспект занятия и выполнить задания.

1. Разложить выражение 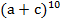по формуле бинома Ньютона.

2. Разложить выражение 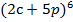по формуле бинома Ньютона.

3. Разложить выражение 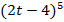по формуле бинома Ньютона.