Метод введения новых переменных

Метод введения новых переменных

Теория:

При решении систем двух уравнений с двумя переменными метод введения новых переменных можно применять двумя способами:

1. вводится одна новая переменная и используется только в одном уравнении системы;

2. вводятся две новые переменные и используются одновременно в обоих уравнениях системы.

Рассмотрим второй способ на примере.

Пример:

Решить систему уравнений {xy(x+y)=6 xy+(x+y)=5
Решение.

Введём новые переменные xy=u, x+y=v.

Тогда систему можно переписать в более простом виде:

{uv=6 u+v=5

Решением системы являются две пары чисел:

{u1=2 v1=3

{u2=3 v2=2

Вернёмся к переменным x и y и решим системы методом подстановки, тогда:

{xy=2 x+y=3 {xy=2 x=3−y1.(3−y)y=2−y2+3y−2=0|⋅(−1)y2−3y+2=0y1=2,y2=12.x=3−yx1=3−2=1x2=3−1=2

{xy=3x+y=2{xy=3x=2−y(2−y)y=3−y2+2y−3=0D<0∅

Ответ: (1;2) и (2;1)

Графический метод

Теория:

Алгоритм решения системы двух уравнений с двумя неизвестными графическим методом:

1. строим график первого уравнения;

2. строим график второго уравнения;

3. находим точки пересечения графиков (координаты каждой точки пересечения служат решением системы уравнений).

Пример:

Решить систему уравнений {x2+y2=9 y−x=−3
Решение.

1. Построим график уравнения x2+y2=9.

Графиком уравнения является окружность с центром в начале координат и радиусом 3.

2. Построим график уравнения y=x−3 (выразили y).

Это прямая, для построения которой найдём две точки (0;−3) и (3;0).

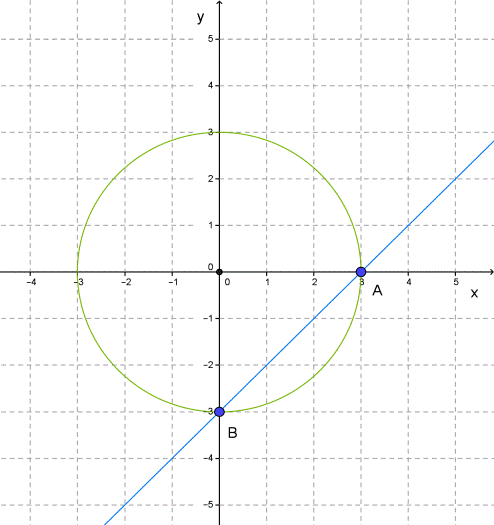
3. Окружность и прямая пересекаются в точках A и B.
Точка A имеет координаты (3;0), а точка B — координаты (0;−3).

Пары чисел (3;0) и (0;−3) являются решениями обоих уравнений системы, а значит, и решениями системы уравнений.

Ответ: (3;0) и (0;−3).