Контрольная работа на тему «Комбинаторика и теория вероятности»

Контрольная работа на тему «Комбинаторика и теория вероятности»

Задание 1. Вычислить:

А)

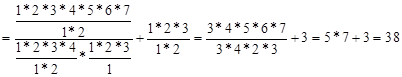
Б)

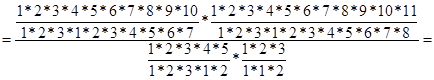
Задание 2.Выясните, сколько различных слов можно составить перестановкой букв из слов
А) БИССЕКТРИСА

Всего 11 букв. Пользуемся формулой перестановок n! И получаем 11!=1*2*3*4*5*6*7*8*9*10*11=39916800

Б) ЭКЗАМЕН

Всего 7 букв. Пользуемся формулой перестановок n! И получаем 7!=1*2*3*4*5*6*7=5040

Задание 3.

Студенты группы изучают 9 дисциплин по 3 пары ежедневно. Сколько существует способов, чтобы распределить пары на один день?

Все возможные способы распределения пар на день представляют собой, очевидно, все возможные размещения из 9 элементов по 3. Поэтому их количество равняется:

Задание 4.Рота состоит из трёх офицеров, шести сержантов и 10 рядовых. Сколькими способами можно выделить из них отряд, состоящий из офицера, двух сержантов и пять рядовых?

Здесь порядок не имеет значения.

Чтобы выбрать 1 офицера из 3, используем число сочетаний: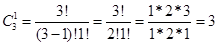

Чтобы выбрать 2 сержантов из 6, используем число сочетаний:

Чтобы выбрать 5 рядовых из 10, используем число сочетаний:

Так как нам нужно выбрать И офицера И сержантов И рядовых, то мы перемножаем варианты: 3*15*252=11340.

Задание 5.В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Вероятность того, что кофе останется в первом автомате равна 1 − 0,3 = 0,7.

Вероятность того, что кофе останется во втором автомате равна 1 − 0,3 = 0,7.

Вероятность того, что кофе останется И в первом И втором автомате равна 0,7*0,7 = 0,49.

Задание 6.В урне 3 белых, 4 красных шаров, 5 красных шаров. Достают два шара. Какова вероятность вытащить наудачу оба красных шара?

Всего возможных варианта выбора двух шаров из 3+4+5=12 в корзине: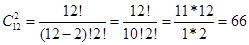

Всего возможных варианта выбора двух красных шаров из имеющихся пяти красных в корзине:

Вероятность того, что достанут два красных шара: 10/66=5/33.