Практическое занятие № 23.. Тема: Непрерывные и периодические функции. Свойства и графики синуса, косинуса, тангенса и котангенса. Преобразования графика функции.. Методические материалы. Теоретическая часть

Практическое занятие № 23.

Тема: Непрерывные и периодические функции. Свойства и графики синуса, косинуса, тангенса и котангенса. Преобразования графика функции.

Цель: Отработка навыков построения графиков тригонометрических функций.

Методические материалы

Теоретическая часть

Преобразование графиков функций.График функции у = f (x+в) получается из графика функции у = f(x) параллельным переносом на (-в) единиц вдоль оси абсцисс.

График функции у = f (x)+а получается из графика функции у = f(x) параллельным переносом на (а) единиц вдоль оси ординат.

График функции у = f (kx) получается из графика функции у = f(x) путем его сжатия в k раз (при k>1) вдоль оси абсцисс.

График функции у = f (kx) получается из графика функции у = f(x) путем его растяжения в k раз.

График функции у = f (kx+b) получается из графика функции у = f(x) путем его параллельного переноса на (-в/k) единиц вдоль оси абсцисс и путем сжатия в k раз (при k>1) или растяжения в k раз (при 0f ( kx+b) = f ( k( x+b/k))

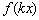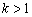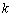Правило: чтобы построить график функции , где , нужно график функции сжать к оси в раз.

Пример 1.Построить график функции .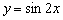

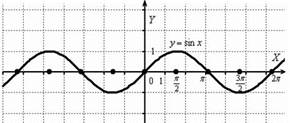
Сначала изобразим график синуса, его период равен :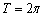

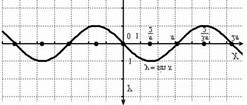
Мысленно возьмём синусоиду в руки и сожмём её к оси 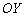в 2 раза:

То есть, график функции 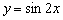получается путём сжатия графика 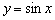к оси ординат в два раза. Логично, что период итоговой функции тоже 0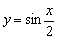

И растягиваем её от оси в 2 раза:

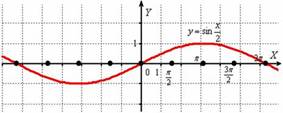
То есть, график функции 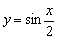получается путём растяжения графика 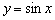от оси ординат в два раза. Период итоговой функции увеличивается в 2 раза: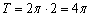

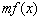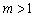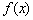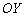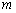Правило: чтобы построить график функции , где , нужно график функции растянуть вдоль оси в раз.

2) Если ФУНКЦИЯ умножается на число 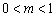, то происходит сжатие её графика вдоль оси ординат.

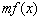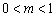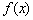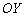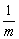Правило: чтобы построить график функции , где , нужно график функции сжать вдоль оси в раз.

Пример 3. Построить графики функций .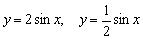

Берём синусоиду:

И вытягиваем её вдоль оси 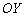в 2 раза:

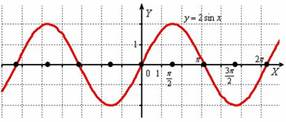
Период функции 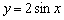не изменился и составляет 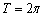, а вот значения (все, кроменулевых) увеличились по модулю в два раза

Ход работы:

1. Рассмотреть теоретический материал и примеры по указанной теме.

2. Решить задания, указанные в практической части, оформить решение в тетради для практических работ.

Практическая часть

Задание.Построить график функции:

1. y=sinx+1 - сдвиг на 1 единицу вверх по оси Оу

2. y=tg(x-p/2) – сдвиг по оси Ох вправо на p/2

3. y=1/2 cosx – уменьшение ординат в 2 раза

4. y= -cosx – симметричное отображение от оси Ох

5. y=-sinx – симметричное отображение от оси Оу