Преподаватель - Брыкало А.А.. Конспект урока «Математика». Группа 5 «Механизация сельского хозяйства». Ход урока

Преподаватель - Брыкало А.А.

brukalo_aa@mail.ru

https://vk.com/id399759339

Конспект урока «Математика»

Группа 5 «Механизация сельского хозяйства»

Тема: «Уравнения и неравенства с двумя переменными»

Форма работы:индивидуальная, электронное обучение

Тип урока:урок изучения нового материала

Продолжительность урока: 2 часа

Цель урока: ввести понятие уравнений и неравенств с двумя переменными, показать способы их решения

Используемая литература:

Учебник: Математика. Алгебра и начала математического анализа. 10-11 классы: учебник для общеобразовательных организаций: базовый и углубленные уровни./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение, 2018г

Интернет-ресурсы:

Методика преподавания математики http://methmath.chat.ru/

Ход урока

Организационный этап:

Мотивационный модуль

Ребята, сегодня на уроке мы вспомним что такое линейные уравнения и неравенства с двумя переменными; системы линейный уравнений и неравенств, а также научимся изображать множество на плоскости, задаваемое линейным уравнением и неравенством.

Историческая справка:

Уравнения, а также системы уравнений имеют давнюю историю. Нам известно, что уже в Древнем Вавилоне и Индии повседневные задачи, связанные с земляными работами или планированием военных расходов, а также астрономическими наблюдениями решались с помощью уравнений и их систем.

В то время еще не существовало привычного нам формального языка математики. Вавилоняне, также, как и индусы не использовали в своих трактатах привычные нам «икс» и «игрек». Не обозначали степень надстрочными индексами. И т.д. Их уравнения записаны в виде текстовых задач. Также, как и решения, не похожи на современные, а скорее напоминают цепочку логических рассуждений.

Вместе с тем, если перевести в привычный нам вид те уравнения, которые умели решать в Древнем Вавилоне, то мы увидим:

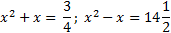И в древнем индийском манускрипте «Ариабхаттиам», датируемом 499 годом нашей эры, также встречаются задачи, решаемые с помощью квадратных уравнений. Индийские мудрецы (слово ученый тоже еще не существовало) уже не ограничивались решением конкретных житейских задач, но и работали над решением квадратного уравнения в общем виде.

Привычный нам вид уравнения обретают только в конце шестнадцатого века, благодаря трудам Франсу Виета (1540 – 1603 гг.). Именно он, помимо прочих своих научных достижений обладает и неофициальным титулом «создатель алгебры». Поскольку разработал и активно внедрял символический язык алгебры – те самые, привычные нам «иксы и игреки».

Основная часть:

Объясняющий модуль

Теоретический материал для самостоятельного изучения

План урока:

1. Линейные уравнения с двумя переменными

2. Линейные неравенства с двумя переменными

1. Линейные уравнения с двумя переменными.

Уравнение вида ах + by +с =0, где а,b,с – некоторые числа, называется линейным уравнением с двумя переменными х и у.

Решением уравнения ах + by +с =0, где а,b,с – некоторые числа, называется пара значений обращающая уравнение в верное числовое равенство.

Если одновременно а 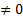и b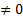, то уравнение ах + by +с =0 является уравнением некоторой прямой. Для построения прямой достаточно найти две точки этой прямой.

Уравнение с двумя неизвестными может:

а) иметь одно решение. Например, уравнение x² + 5y² = 0 имеет единственное решение (0; 0);

б) иметь несколько решений. Например, (5 -|x|)² + (|y| – 2)² = 0 имеет 4 решения: (5; 2), (-5; 2), (5; -2), (-5; -2);

в) не иметь решений. Например, уравнение x² + y² + 1 = 0 не имеет решений;

г) иметь бесконечно много решений. Например, x + y = 3. Решениями этого уравнения будут являться числа, сумма которых равна 3. Множество решений данного уравнения можно записать в виде (k; 3 – k), где k – любое действительное число.

Пример 1.

Решить уравнение: xy – 2 = 2x – y.

Группируем слагаемые с целью разложения на множители:

(xy + y) – (2x + 2) = 0.

Из каждой скобки вынесем общий множитель:

y(x + 1) – 2(x + 1) = 0;

(x + 1)(y – 2) = 0.

Имеем:

y = 2, x – любое действительное число или x = -1, y – любое действительное число.

Таким образом, ответом являются все пары вида (x; 2), x ? R и (-1; y), y ? R.

Пример 2.

Построить график уравнения 2х+у =1

Решение: у = -2х + 1

Если х=0, то у=1;

Если х=2, то у=-3.

На координатной плоскости отметим точки с координатами (0;1) и (2;-3).

Через две точки на плоскости проведем прямую. Полученная прямая является геометрической моделью уравнения 2х+у =1. (График постройте самостоятельно)

2. Линейные неравенства с двумя переменными.

Линейным неравенством с двумя переменными называется неравенство вида ах + bу + с < 0 или ах + bу + с > 0, где х и у – переменные, а, b, c – некоторые числа.

Решением неравенства с двумя переменными называется пара значений переменных, обращающая его в верное неравенство.

Является ли пара (2;1) решением неравенства 5х + 2у > 4 . Является, т.к. при подстановке в него вместо х числа 2, а вместо у числа 1 получается верное равенство 10 + 2 > 4.

Если каждое решение неравенства с двумя переменными изобразить точкой в координатной плоскости, то получится график этого неравенства. Он является некоторой фигурой.

Тренировочный модуль.

Пример 3.

Найти множество точек координатной плоскости, удовлетворяющих неравенству 3х – 2у +6 > 0.

Уравнение 3х – 2у +6 = 0 является уравнением прямой, проходящей через точки (-2; 0) и (0; 3).

Пусть точка М₁(х₁,у₁) лежит в заштрихованной полуплоскости (ниже прямой

3х – 2у +6 = 0, а М₂(х₁,у₂) лежит на прямой 3х – 2у +6 = 0. Тогда 2у₂ – 3х₁ – 6 = 0, а 2у₁ – 3х₁ – 6 < 0, т.к. у₁< у₂

Изобразим множество точек координатной плоскости, удовлетворяющих неравенству 3х – 2у +6 > 0 штриховкой (рис. 1)

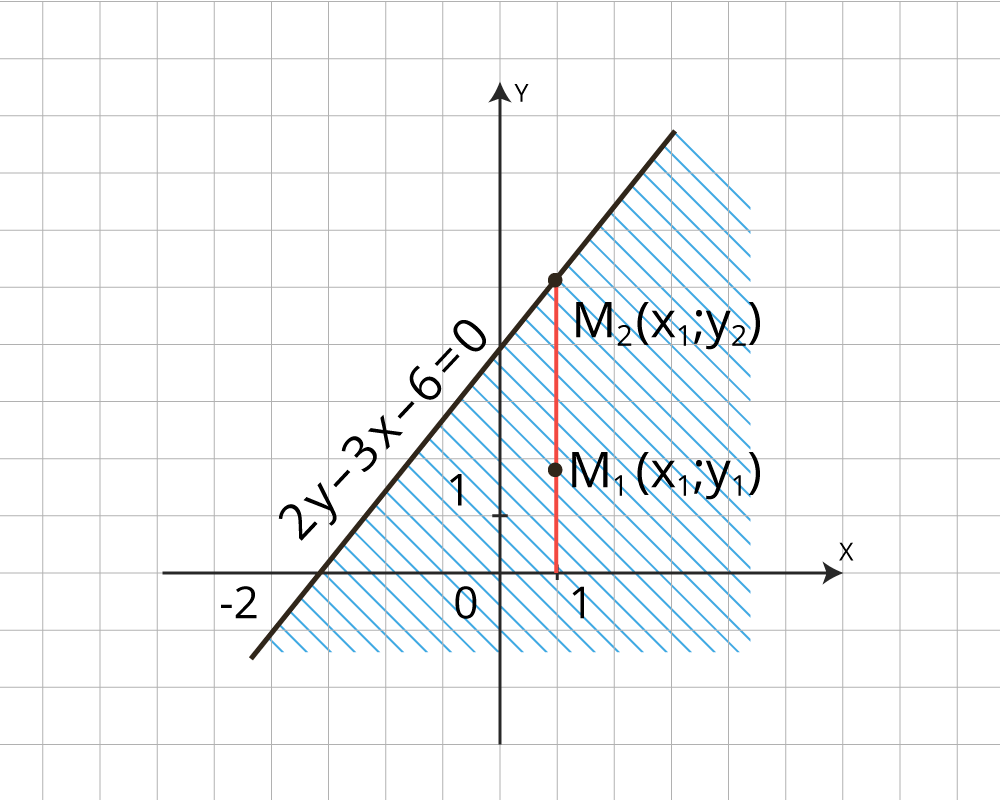
Рисунок 1 – решение неравенства 3х – 2у +6 > 0

Если в линейном неравенстве с двумя переменными знак неравенства заменить знаком равенства, то получится линейное уравнение ах + by +с =0, графиком которого является прямая при условии, что 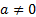и 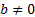. Прямая разбивает плоскость на две полуплоскости. Одна из них является графиком неравенства ах + bу + с < 0, а другая – графиком неравенства ах + bу + с > 0

Чтобы решить неравенство ах + bу + c < 0 или aх + bу + c > 0, достаточно взять какую-нибудь точку М₁(х₁; у₁), не лежащую на прямой aх + bу + c = 0, и определить знак числа aх₁ + bу₁ + c.

Пример 4.

Изобразите в координатной плоскости множества решений неравенства 2х + 3у<6

Начертим график уравнения 2х + 3у = 6.

Пара (0;0) является решением неравенства 2х + 3у < 6, и принадлежит нижней полуплоскости, значит графиком неравенства 2х + 3у < 6 является нижняя полуплоскость (рис. 2).

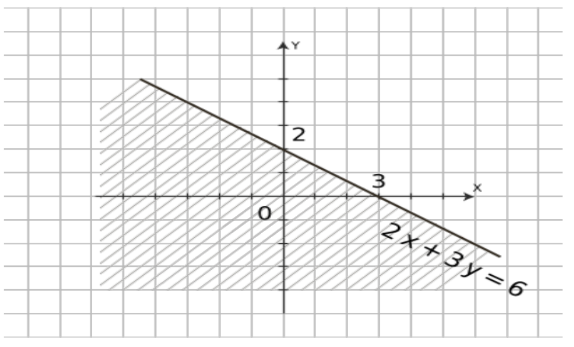
Рисунок 2 – решение неравенства 2х + 3у < 6

Пример 5.

Изобразите в координатной плоскости множества решений неравенства

3х-2у+6 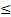0.

Начертим график уравнения 3х – 2у + 6 = 0

Отметим в какой-нибудь полуплоскости, например, точку (1;2).

Пара (1;2) не является решением неравенства 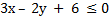и принадлежит нижней полуплоскости, значит графиком неравенства 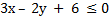является верхняя полуплоскость вместе с прямой 3х – 2у + 6 = 0. 9 (рис. 5)

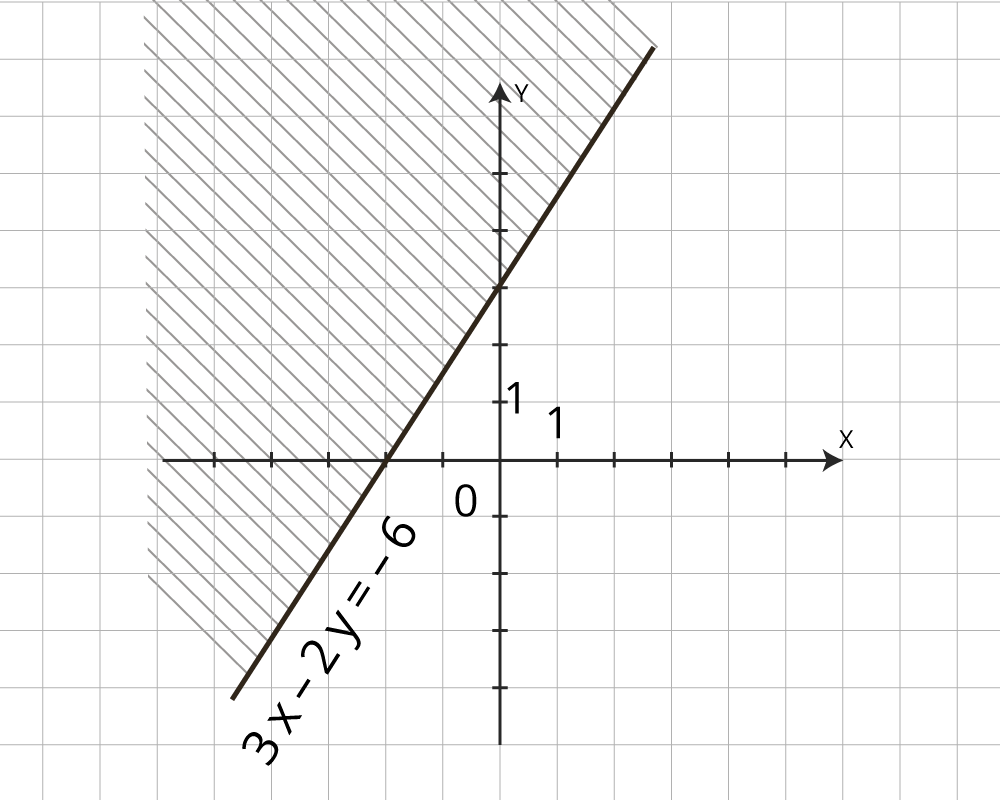
Рисунок 5 – решение неравенства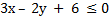

Домашнее задание.

1. Составить опорный конспект по теме.

2. Решить следующие задания:

Пример 1. 2х+3у > 0

Пример 2. Является ли решением уравнения 3х+ 4у=12 пара чисел а)2;1 б) 1; 2,25