Конспект урока математики . Группа 92. Форма работы: индивидуальная, электронное обучение.. Организационный этап. Мотивационный модуль.. Объясняющий модуль. Повторение. Методические рекомендации

Преподаватель Липницкая В.Н. lipnickaya.1956@mail.ru

Конспект урока математики

Дата: 3.05.2021

Группа 92

Курс 2

Тема: Практическое занятие №70«Решение логарифмических уравнений и неравенств»

Форма работы: индивидуальная, электронное обучение.

Тип урока: урок совершенствования знаний, умений и навыков по теме «Логарифмические уравнения и неравенства»

Цель урока:совершенствовать навыки решения заданий по теме «Логарифмические уравнения и неравенства»

Изучаемая литература:Математика : алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа.

10-11 классы: учеб.для общеобразоват.организаций: базовый и углубл.уровени./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение , 2018г

Интернет – ресурсы:http://www bymath.net

Ход урока:

1.Организационный этап. Мотивационный модуль.

Ребята, на этом уроке вы повторите материал по теме «Логарифмические уравнения и неравенства», выполните практическую работу по данной теме.

2.Объясняющий модуль. Повторение

Методические рекомендации

Вспомните определение логарифма.

Повторите схему решения логарифмических уравнений вида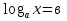

Логарифмическая функция возрастает (или убывает) на промежутке ( 0; +∞) и принимает на этом промежутке все действительные значения. По теореме о корне для любого вданное уравнение имеет единственное решение. Из определения логарифма следует, чтоа^вявляется таким решением.

Пример: решите уравнение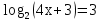

Решение: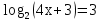

4х +3 = 2³

4х = 8-3

4х = 5

х =1 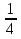Ответ: 1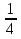

Решение логарифмических неравенств основано на том, что функция

у = 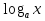при а>1 является монотонно возрастающей на своей области определения, а при 0<a<1монотонно убывающей на своей области определения.

При переходе от простейшего неравенства к равносильным системам неравенств, не содержащих знака логарифма следует учитывать область допустимых значений исходного неравенства.

При решении логарифмических неравенств пользуйтесь следующей схемой:

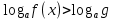(x)

a > 1 0 < a < 1

f(x) > g(x) f(x) < g(x)

g(x) > 0 f(x) > 0

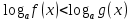
1 0 < a < 1

f(x) < g(x) f(x) > g(x)

f(x) > 0 g(x) > 0

Пример: 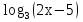< 2

Решение: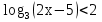

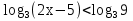
Функция у =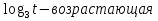

2х-5< 9

2х-5 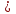0;

2х <14

2х >5;

х <7

х>2,5 х 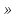(2,5; 7)

Ответ: х 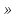(2,5; 7)

Практическое занятие №70

Тема «РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ»

Цель:систематизировать знания о решении логарифмических уравнений и неравенств, углубить знания при решении уравнений и неравенств, опираясь на свойства

Вариант 1

1. Решите уравнения: а) 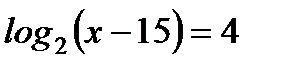; б) ;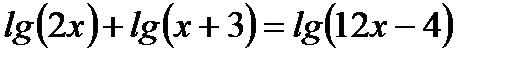

в) .

2. Решите неравенство: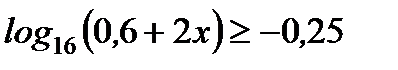

Вариант 2

1. Решите уравнения: а) 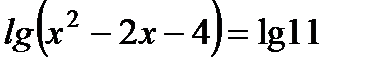; б) ;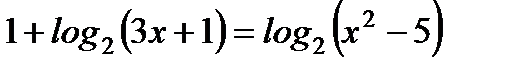

в) .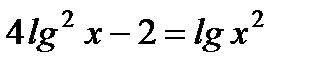

2. Решите неравенство: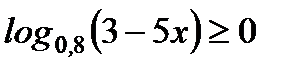

Выполненную работу отправить ЛС в ВК