
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Школа одаренных. Итоговая контрольная работа за 4 класс по математике. 2021 год. Школа одаренных. Итоговая контрольная работа за 4 класс по математике. 2021 год
Школа одаренных
Итоговая контрольная работа за 4 класс по математике. 2021 год
Задача 1.Разрежьте данную фигуру на три равных части:
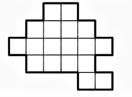
Задача 2.За круглым столом, где сидеть могли только рыцари и лжецы (два племени), сидели 10 человек. Каждый из них по очереди сказал «два человека слева от меня и два человека справа от меня из одного и того же племени». Приведите два примера, сколько могло сидеть рыцарей за столом.
Примечание:Рыцари всегда говорят правду, лжецы всегда лгут.
Задача 3.Шахматный конь стоял на черной клетке. На какой по цвету клетке он окажется через 10 ходов? Докажите, что так будет всегда.
Задача 4.В школе к выпускному готовились подарок для детей: на 12 стульчиках, стоящих в круг, были коробочки с конфетами. Количество конфет, лежащих в двух соседних коробках, отличалась на 1. Могло ли во всех коробках быть 999 конфет?
Задача 5.Аня и Миля играют в такую игру: они по очереди пишут цифры восьмизначного числа (Аня – первую, Миля – вторую, Аня – третью, Миля – четвертую и так далее). Аня выигрывает, если полученное число не делится на 9, Миля – если полученное число делится. Кто победит при правильной игре?
Школа одаренных
Итоговая контрольная работа за 4 класс по математике. 2021 год
Задача 1.Разрежьте данную фигуру на три равных части:
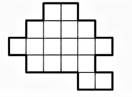
Задача 2.За круглым столом, где сидеть могли только рыцари и лжецы (два племени), сидели 10 человек. Каждый из них по очереди сказал «два человека слева от меня и два человека справа от меня из одного и того же племени». Приведите два примера, сколько могло сидеть рыцарей за столом.
Примечание:Рыцари всегда говорят правду, лжецы всегда лгут.
Задача 3.Шахматный конь стоял на черной клетке. На какой по цвету клетке он окажется через 10 ходов? Докажите, что так будет всегда.
Задача 4.В школе к выпускному готовились подарок для детей: на 12 стульчиках, стоящих в круг, были коробочки с конфетами. Количество конфет, лежащих в двух соседних коробках, отличалась на 1. Могло ли во всех коробках быть 999 конфет?
Задача 5.Аня и Миля играют в такую игру: они по очереди пишут цифры восьмизначного числа (Аня – первую, Миля – вторую, Аня – третью, Миля – четвертую и так далее). Аня выигрывает, если полученное число не делится на 9, Миля – если полученное число делится. Кто победит при правильной игре?
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|