
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Для задания №4. Задание на курсовую работу по дисциплине. Задание №2.
Для задания №4
N1- номер строки в таблице3, N2- номер строки в таблице4, N3 – номер схемы на рисунке2.
Структурно работа состоит из введения, 4 разделов, заключения, источников использованной литературы. Общий объём работы 42-47 страниц. Работа иллюстрируется рисунками. Библиографический список должен включает не менее 7 источников.
Задание на курсовую работу по дисциплине
“Теоретические основы электротехники”
Тема: “Расчет разветвленных линейных электрических цепей с сосредоточенными параметрами”
Задание №1.
1. Расчет линейной электрической цепи с постоянными напряжениями и токами.
e1(t)=E1
e2(t)=E2
e3(t)= E1
j(t)= J
При выполнении этого задания влияние индуктивностей, конденсаторов и магнитная связь не учитывается.
1.1 Изобразить схему, достаточную для расчета токов ветвей, соединяющих узлы,
помеченные буквами, указав их номера и направления. Ввести индексную цифровую нумерацию всех пассивных элементов схемы.
1.2 Определить токи во всех ветвях схемы и напряжение на зажимах источника тока:
1.2.1 По законам Кирхгофа
1.2.2 Методом контурных токов
1.2.3 Методом узловых потенциалов
1.3 Составить баланс вырабатываемой и потребляемой мощностей.
1.4 Определить ток в ветви аЬ:
1.4.2 Методом преобразований.
1.5 Рассматривая цель относительно сопротивления R ветви аЬ как активный
двухполюсник, заменить его эквивалентным генератором, определить параметры
эквивалентного генератора и рассчитать ток в ветви аЬ.
Задание №2.
1. Расчет линейной электрической цепи с гармоническими напряжениями и токами.
e1(t)=√2*E1*sin(ωt+α1)
e2(t)=√2*E2*sin(ωt+α2)
e3(t)=√2*E2*sin(ωt+α1)
j(t)= √2*J*sin(ωt+β)
2.2 Изобразить схему, достаточную для расчета токов ветвей, соединяющих узлы,
помеченные буквами, указав их номера и направления. Ввести индексную нумерацию всех пассивных элементов схемы.
Рассчитать без учета М комплексные сопротивления ветвей, соединяющих узлы, помеченные на схеме буквами и изобразить комплексную схему замещения с этими сопротивлениями для расчета комплексов действующих значений токов ветвей (номера и направления токов сохранить согласно заданию №1, причем параллельное соединение конденсатора и индуктивности, представить в виде одного комплексного сопротивления).
2.3 Не исключая индуктивной связи, определить комплексы действующих значений токов всех ветвей и напряжение на зажимах источника тока
2.3.1 по законам Кирхгофа
2.4 Записать мгновенные значения токов в ветви аЬ и напряжения на зажимах источника тока.
2.5 Рассчитать балансы активной и реактивной мощностей.
2.6 Построить лучевую диаграмму токов и совмещенную с ней топографическую диаграмму напряжений.
2.7 Определить показание вольтметра.
Магнитная связь Мв задании - встречная для четных N3 и согласованная для нечетных N3
Задание №3
3. Расчет линейной электрической цепи с периодическими негармоническими напряжениями и токами
e1(t)=E1+√2*E1*sin(ωt+α1)+ √2*E1/3*sin(3ωt+α1)
e2(t)=E2+√2*E2*sin(ωt+α2)
e3(t)=E1+√2*E2*sin(ωt+α1)+√2*E2/5*sin(3ωt+α1)
j(t)= J+√2*J*sin(ωt+β)
3.1 Рассчитать токи во всех ветвях применением принципа наложения , учитывая, что постоянная составляющая и первая гармоника всех напряжений и токов найдены при расчете 1-го и 2-го заданий соответственно.
3.2 Рассчитать напряжение на зажимах источника тока.
3.3 Определить показание вольтметра:
3.3.1 магнитоэлектрической системы,
3.5 Проанализировать результаты вычислений и сформулировать выводы по заданию.
Задание №4
4. Расчет линейной трехфазной цепи с гармоническими напряжениями и токами.
eA (t)=√2*E*sin(ωt)
eB (t)=√2*E*sin(ωt-1200)
eC (t)=√2*E*sin(ωt-2400)
Изобразить схему, указав номера и направления токов и напряжений во всех фазах. Ввести индексную нумерацию всех пассивных элементов схемы.
4.1.Расчет симметричного режима:
4.1.1преобразовать схему до эквивалентной звезды и определить комплексы
действующих значений напряжений и токов, а также рассчитать показание ваттметра;
4.1.2 в исходной схеме расчетом на одну фазу определить комплексы действующих
значений всех напряжений и токов;
4.1.3. рассчитать балансы активной и реактивной мощностей;
4.1.4. построить совмещенные векторные диаграммы для всех напряжений и токов.
4.2. Расчет несимметричного режима:
4.2.1 упростить схему и определить комплексы действующих значений напряжений и
токов, а также рассчитать показание ваттметра;
4.2.2 в исходной схеме определить неизвестные комплексы действующих значений
напряжений и токов;
4.2.3 рассчитать балансы активной и реактивной мощностей;
4.2.4 построить совмещенные векторные диаграммы для всех напряжений и токов.
4.3 Проанализировать результаты вычислений, сравнить симметричный и
несимметричный режимы, сформулировать выводы по работе. При выполнении задания необходимо учитывать, что для схем с номерами 1,3,6,8 симметричный вариант схемы соответствует замкнутому состоянию ключа К. Для остальных схем - разомкнутому состоянию ключа К. Для схем с номерами 1,3,6,8 несимметричный вариант схемы соответствует разомкнутому состоянию ключа К. Для остальных схем - замкнутому состоянию ключа К.
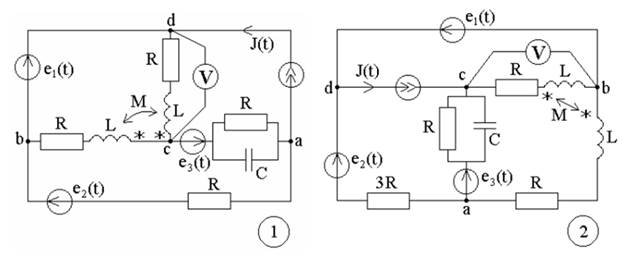
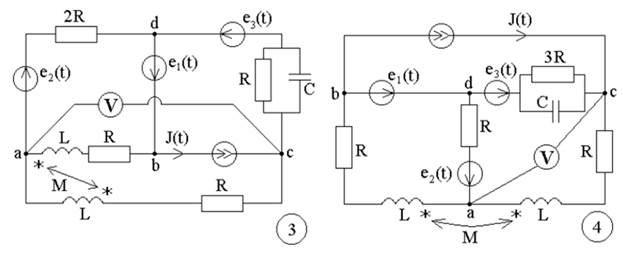
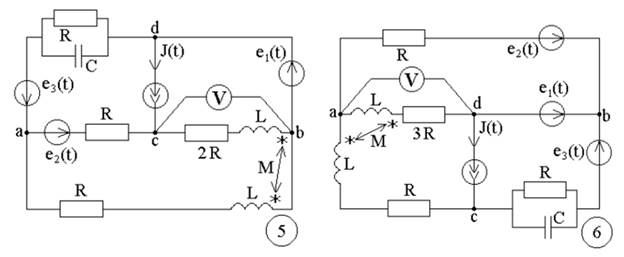
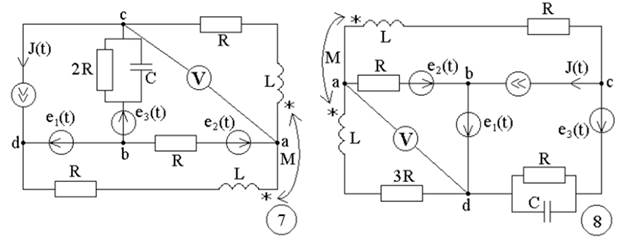
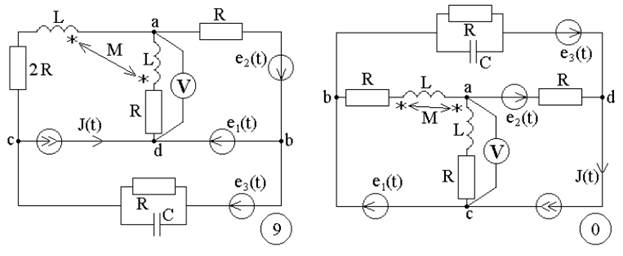
Рисунок 1- Варианты схем к заданиям №1, 2,3
Таблицы значений параметров элементов схем рисунка 1 для заданий №1,2,3
Таблица 1 Таблица 2
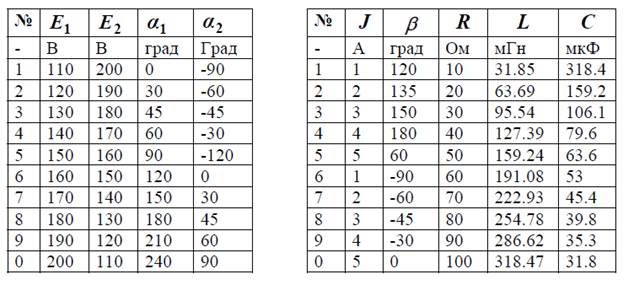
Таблицы значений параметров элементов схем рисунка 2 для задания №4
Таблица 3 Таблица 4
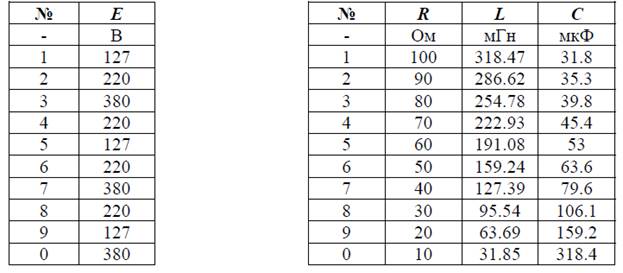
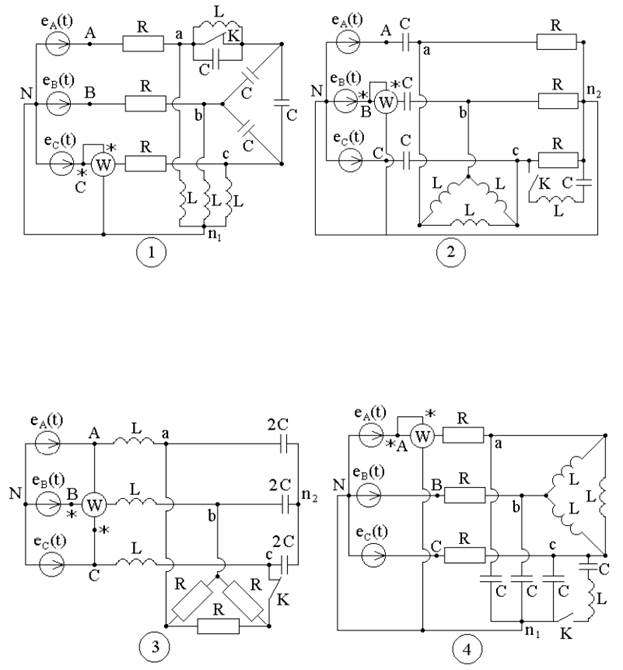
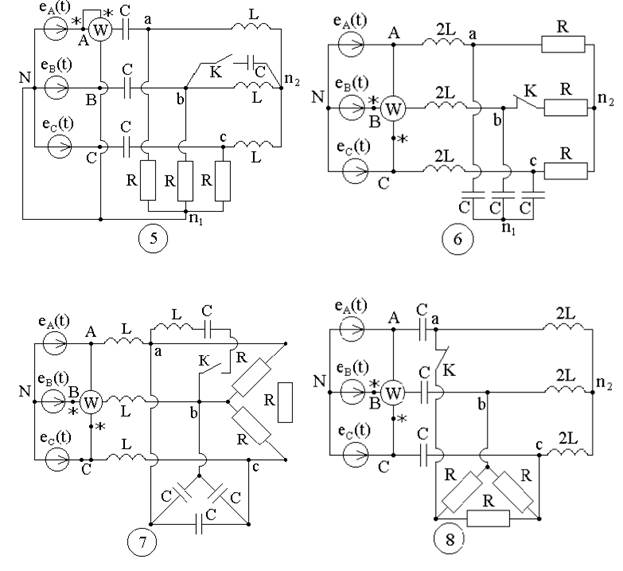
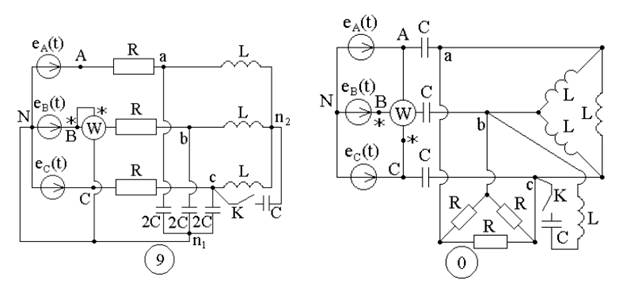
Рисунок 2 - Варианты схем к заданию №4
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|