
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры и разбор решения заданий тренировочного модуля
Урок № 132
Тема:Уравнение cos(x) = a
Цель урока: рассмотреть и отработать навыки решения тригонометрических уравнений -
· решение уравнения 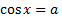 для табличных значений
для табличных значений
· арккосинус числа, простейшие тождества с арккосинусом
· решение уравнения sin x = a для произвольных значений
· решение простейших тригонометрических уравнений;
· решение уравнения вида 
· решение уравнения вида 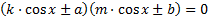 ;
;
· решение уравнения вида 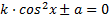 ;
;
· вычисление значений арккосинуса числа.
Ход урока
1. Изучение нового материала
С этого урока мы начинаем изучать уравнения и неравенства, которые содержат косинус, синус, тангенс и котангенс переменной. Решение таких уравнений и неравенств - нахождение значений переменной по заданному значению косинуса, синуса, тангенса или котангенса.
Начнем мы изучение тригонометрических уравнений с уравнения
вида cos x = a.
Арккосинусом числа m 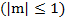 называется такое число α, что:
называется такое число α, что:  и
и  .
.
Арккосинус числа m обозначают: 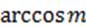 .
.
1. Решение тригонометрического уравнения  на первом этапе целесообразно выполнять с использованием тригонометрической окружности. Из рисунка видно, что при
на первом этапе целесообразно выполнять с использованием тригонометрической окружности. Из рисунка видно, что при 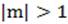 , таких точек нет, при
, таких точек нет, при 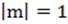 , такая точка одна, при
, такая точка одна, при 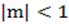 , таких точек две.
, таких точек две.
Так как 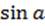 является абсциссой точки М(α) координатной окружности, то для решения уравнения
является абсциссой точки М(α) координатной окружности, то для решения уравнения 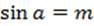 нужно сначала найти на этой окружности точки, имеющие абсциссу m, то есть точки пересечения окружности с прямой x=m. Если
нужно сначала найти на этой окружности точки, имеющие абсциссу m, то есть точки пересечения окружности с прямой x=m. Если 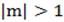 , то таких точек нет, если
, то таких точек нет, если 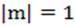 , то такая точка одна, если
, то такая точка одна, если 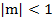 , то таких точек две.
, то таких точек две.
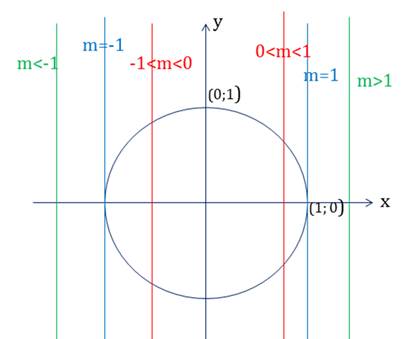
Рисунок 1 – Точки пересечения прямой x = m с тригонометрической окружностью
Рассмотрим решение уравнения 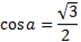 .
.
Прямая  пересекает тригонометрическую окружность в двух точках: M(π/6) и N(-π/6).
пересекает тригонометрическую окружность в двух точках: M(π/6) и N(-π/6).

Рисунок 2 – Решение уравнения 
Точка M(π/6) соответствует всем числа вида 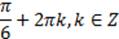 .
.
Точка N(-π/6) соответствует всем числа вида 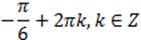 .
.
Таким образом, решение уравнения 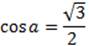 можно записать так:
можно записать так:
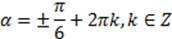 .
.
Ответ: 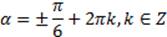
Чтобы уметь решать уравнение  для произвольных значений m, вводится понятие арккосинуса.
для произвольных значений m, вводится понятие арккосинуса.
Арккосинусом числа m 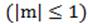 называется такое число α, что:
называется такое число α, что: 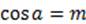 и
и 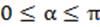 .
.
Арккосинус числа m обозначают: 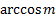
Для 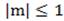

Если 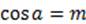 и
и 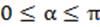 , то
, то 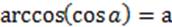 .
.
Два простейших тождества для арккосинуса.
1. 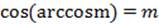 для любого m:
для любого m: 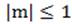
2. 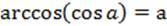 для любого α:
для любого α: 
Из рисунка видно, что 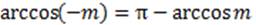 .
.
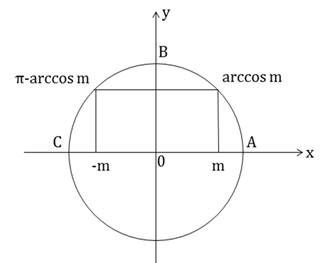
Рисунок 3 – Связь между 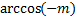 и
и 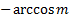
Решением уравнения 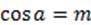 являются все числа вида
являются все числа вида

Примеры и разбор решения заданий тренировочного модуля
№1.Решите уравнение 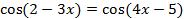 .
.
В ответ запишите наименьший положительный корень.
Решение:
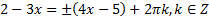

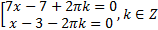

При  получаем
получаем  .
.
При увеличении значений k значение первого корня будет отрицательным, а значение второго корня будет увеличиваться.
При уменьшении значений k значение первого корня будет увеличиваться, а значение второго корня будет отрицательным. Поэтому наименьшее положительное значение корня 1.
Ответ: 1
№2.Решите уравнение 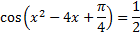 . Определите, сколько решений имеет это уравнение при:
. Определите, сколько решений имеет это уравнение при:
1. k=-3
Ответ: 0
1. k=0
Ответ: 4
1. k=2
Ответ: 4
Решение:
Запишем решение данного уравнения в виде:

Тогда: 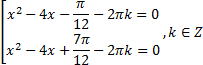
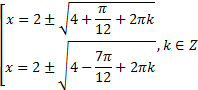
Первое уравнение имеет решение, если  . То есть
. То есть 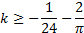 , или
, или 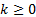 .
.
Второе уравнение имеет решение, если 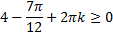 . То есть
. То есть 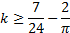 , или
, или 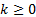 .
.
Поэтому при 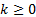 уравнение будет иметь 4 решения, а при
уравнение будет иметь 4 решения, а при 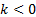 ни одного.
ни одного.
Домашняя работа:
Задание 1.

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|