
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ. Урок Методы решения однородных тригонометрических уравнений.. Однородные тригонометрические иуравнения.. Алгоритм решения однородного уравнения второй степени a sin2 x + b sin x cos x + c cos2 x = 0.. Условие: в уравнении должно б
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
Урок Методы решения однородных тригонометрических уравнений.
Однородные тригонометрические иуравнения.
Цели: изучить понятие однородного тригонометрического уравнения ;освоить навыки решения однородных тригонометрических уравнений.
Однородное тригонометрическое уравнение – это уравнение двух видов:
a sin x + b cos x = 0 (однородное уравнение первой степени)
либо
a sin2 x + b sin x cos x + c cos2 x = 0 (однородное уравнение второй степени).
Отличительные признаки однородных уравнений:
а) все одночлены имеют одинаковую степень,
б) свободный член равен нулю,
в) в уравнении присутствуют степени с двумя различными основаниями
Алгоритм решения однородного уравнения первой степени a sin x + b cos x = 0:
| 1) разделить обе части уравнения на cos x 2) решить получившееся выражение |
Пример: Решим уравнение 2 sin x – 3 cos x = 0.
Решение.
Разделим обе части уравнения на cos x:
2 sin x- 3 cos x = 0
Делим на cos x
Получаем:
2 tg x – 3 = 0
2 tg x = 3
tg x = 3\2
Ответ: x = arctg  — + πn
— + πn
Алгоритм решения однородного уравнения второй степени a sin2 x + b sin x cos x + c cos2 x = 0.
Условие: в уравнении должно быть выражение вида a sin2 x. Если его нет, то уравнение решается методом разложения на множители.
| 1) Разделить обе части уравнения на cos2 x 2) Ввести новую переменную z, заменяющую tg x (z = tg x) 3) Решить получившееся уравнение |
Пример: Решить уравнение sin2 x – 3 sin x cos x + 2 cos2 x = 0.
Решение.
Разделим обе части уравнения на cos2 x:
sin2 x- 3 sin x cos + 2 cos2 x= 0
Делим на cos2 x
Получаем:
tg2 x – 3 tg x + 2 = 0.
Вместо tg x введем новую переменную z и получим квадратное уравнение:
z2 – 3z + 2 = 0.
Найдем корни:
z1 = 1
z2 = 2.
Значит:
либо tg x = 1,
либо tg x = 2.
Сначала найдем x при tg x = 1:
x = arctg 1 + πn.
x = π/4 + πn.
Теперь найдем x при tg x = 2:
x = arctg 2 + πn.
Ответ: x = π/4 + πn; x = arctg 2 + πn.
Решить уравнения:
1. 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2
2. 1+7cos 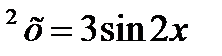
3. 3+sin2x=4 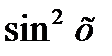
4. Cos2x + 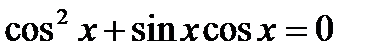
5. 
6. Cos x=sin x
7. 2sinx+cosx=0
8. Sinx=2cos2x
9. 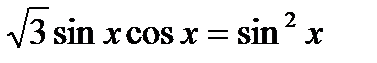
10. Sin4x +sin2x=0
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|