
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Внутривузовская олимпиада по математике, ТУСУР, 2020 год, 1 курс.
Внутривузовская олимпиада по математике, ТУСУР, 2020 год, 1 курс.
ЗАДАЧА 1. На графике 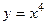 при произвольном
при произвольном 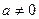 могут быть взяты 3 точки с абсциссами 0,
могут быть взяты 3 точки с абсциссами 0, 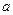 ,
, 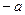 , через них проведена окружность. Найти минимально возможный диаметр окружностей, построенных таким способом.
, через них проведена окружность. Найти минимально возможный диаметр окружностей, построенных таким способом.
ЗАДАЧА 2. На прямой 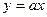 при любом параметре
при любом параметре 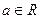 есть точка, ближайшая к точке (С,0). Найти уравнение кривой, которую образуют все такие точки при
есть точка, ближайшая к точке (С,0). Найти уравнение кривой, которую образуют все такие точки при 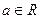 .
.
ЗАДАЧА 3. Найти односторонний предел 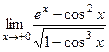 .
.
ЗАДАЧА 4. Найти, какую максимальную долю объёма может занимать прямой круговой конус, вписанный в шар радиуса 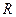 .
.
ЗАДАЧА 5. Прямая 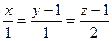 является проекцией прямой
является проекцией прямой 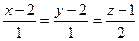 на плоскость
на плоскость 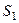 , а прямая
, а прямая 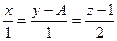 является проекцией этой же прямой на плоскость
является проекцией этой же прямой на плоскость 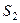 . Найти параметр
. Найти параметр 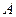 , при котором плоскости
, при котором плоскости 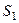 и
и 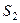 ортогональны.
ортогональны.
Решения задач
Задача 1. На графике 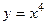 при произвольном
при произвольном 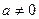 могут быть взяты 3 точки с абсциссами 0,
могут быть взяты 3 точки с абсциссами 0, 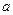 ,
, 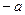 , через них проведена окружность. Найти минимально возможный диаметр окружностей, построенных таким способом.
, через них проведена окружность. Найти минимально возможный диаметр окружностей, построенных таким способом.
Решение.
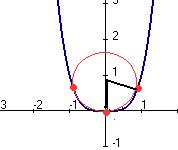
Пусть радиус равен 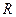 . Тогда расстояние от точки . Тогда расстояние от точки 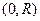 до точек до точек 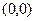 , , 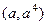 и и 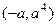 равно равно 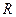 . По теореме Пифагора, . По теореме Пифагора, 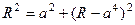 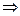 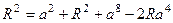 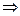
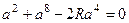 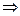 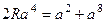 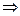 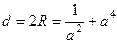 . .
| 
|
Найдём экстремум этой величины по 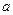 .
.
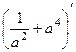 =
= 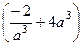 = 0
= 0 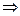
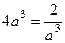
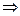
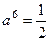
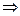
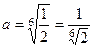 .
.
При этом 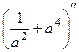 =
= 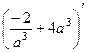 =
= 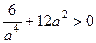 , поэтому минимум, а не максимум.
, поэтому минимум, а не максимум.
Теперь найдём 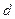 .
. 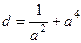 =
= 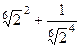 =
= 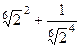 =
= 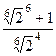 =
=
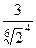 =
= 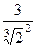 =
= 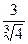 . Ответ.
. Ответ. 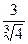 .
.
ЗАДАЧА 2. На прямой 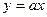 при любом параметре
при любом параметре 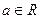 есть точка, ближайшая к точке (С,0). Найти уравнение кривой, которую образуют все такие точки при
есть точка, ближайшая к точке (С,0). Найти уравнение кривой, которую образуют все такие точки при 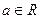 .
.
РЕШЕНИЕ. Пусть точка является ближайшей к (С,0). Тогда вектор 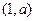 , расположенный на прямой, перпендикулярен вектору, соединяющему точку
, расположенный на прямой, перпендикулярен вектору, соединяющему точку 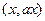 с точкой
с точкой 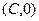 , то есть вектору
, то есть вектору 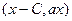 . Скалярное произведение векторов
. Скалярное произведение векторов 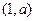 и
и 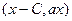 равно 0, то есть
равно 0, то есть 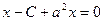 . Отсюда можно найти абсциссу точки, которая является ближайшей к указанной.
. Отсюда можно найти абсциссу точки, которая является ближайшей к указанной. 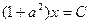 ,
, 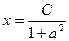 . Тогда
. Тогда 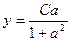 . Это параметрические уравнения кривой. Чтобы найти неявное уравнение кривой, нужно устранить зависимость от параметра, то есть выразить
. Это параметрические уравнения кривой. Чтобы найти неявное уравнение кривой, нужно устранить зависимость от параметра, то есть выразить 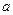 из одного уравнения и подставить во второе. Из первого уравнения:
из одного уравнения и подставить во второе. Из первого уравнения: 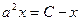 ,
, 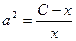 ,
, 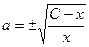 .
.
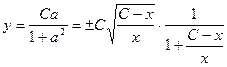 =
= 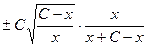 =
= 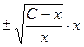 =
= 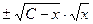
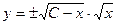 тогда
тогда 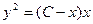 ,
, 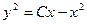 ,
, 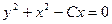 , выделим полный квадрат:
, выделим полный квадрат: 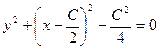 ,
, 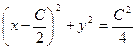 .
.
Таким образом, кривая, состоящая из точек, являющихся ближайшими к (С,0), есть окружность с центром в точке 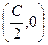 радиуса
радиуса 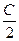 .
.
Чертёж:
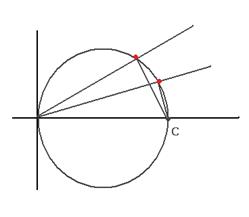
ОТВЕТ. 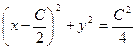 окружность с центром в точке
окружность с центром в точке 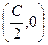 радиуса
радиуса 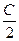 .
.
ЗАДАЧА 3. Найти односторонний предел 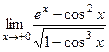 .
.
РЕШЕНИЕ.
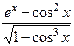 =
= 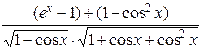 =
= 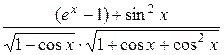 =
=
= 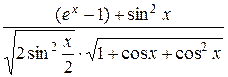 =
= 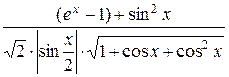 .
.
Выражение 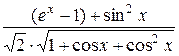 в окрестности точки
в окрестности точки 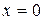 имеет положительно.
имеет положительно.
В правой полуокрестности верно 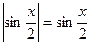 , поэтому нужно вычислить
, поэтому нужно вычислить
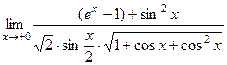
Разобьём на 2 множителя, предел одного из них вычисляется непосредственной подстановкой 0, второй с помощью эквивалентности бесконечно малых.
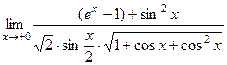 =
= 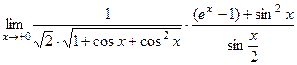
 =
=
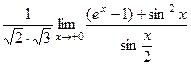 =
= 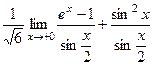 =
= 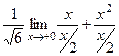 =
= 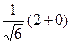 =
= 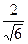 =
= 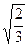 .
.
ОТВЕТ. 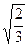 .
.
ЗАДАЧА 4. Найти, какую максимальную долю объёма может занимать прямой круговой конус, вписанный в шар радиуса 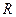 .
.
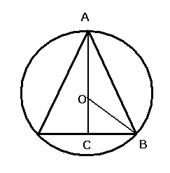
РЕШЕНИЕ. Объём шара 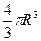 . Для вписанного в шар конуса, высота
. Для вписанного в шар конуса, высота 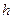 и радиус
и радиус 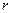 взаимосвязаны между собой. Расстояние от центра основания конуса до центра шара есть
взаимосвязаны между собой. Расстояние от центра основания конуса до центра шара есть 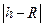 (см.чертёж - вид сбоку, на чертеже это ОС). Отрезок ВС на чертеже равен
(см.чертёж - вид сбоку, на чертеже это ОС). Отрезок ВС на чертеже равен 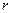 - радиусу основания конуса. Далее, по теореме Пифагора (ОС)2+(ВС)2 = (ОВ)2.
- радиусу основания конуса. Далее, по теореме Пифагора (ОС)2+(ВС)2 = (ОВ)2.
То есть, 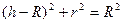 , следовательно,
, следовательно, 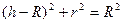 ,
, 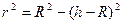 ,
,
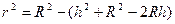 ,
, 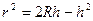 . По известным формулам, объём конуса равен
. По известным формулам, объём конуса равен 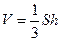 , а площадь основания
, а площадь основания 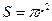 , тогда
, тогда 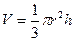 ,
, 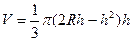 =
= 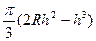 . Найдём экстремум по
. Найдём экстремум по 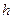 .
.
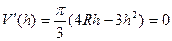 ,
, 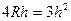 ,
, 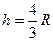 .
.
Легко убедиться, что это именно максимум, так как вторая производная отрицательна: 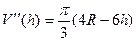 , при
, при 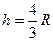
получается 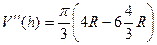 =
= 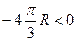 .
.
При этом значении объём конуса равен 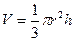 =
= 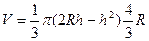 =
= 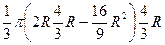 =
= 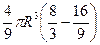 =
= 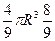 =
= 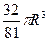 .
.
Нужно найти отношение объёма конуса к объёму шара, поэтому поделим друг на друга объёмы этих тел: 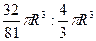 =
= 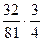 =
= 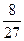 .
.
ОТВЕТ. 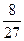 .
.
ЗАДАЧА 5. Прямая 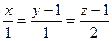 является проекцией прямой
является проекцией прямой 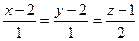 на плоскость
на плоскость 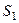 , а прямая
, а прямая 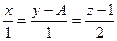 является проекцией этой же прямой на плоскость
является проекцией этой же прямой на плоскость 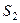 . Найти параметр
. Найти параметр 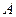 , при котором плоскости
, при котором плоскости 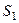 и
и 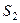 ортогональны.
ортогональны.
Решение.Из строения знаменателей дробей этих канонических уравенений видно, что все направляющие векторы прямых совпадают.
Найдём уравнение плоскости 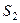 , которая содержит проекцию, при произвольном
, которая содержит проекцию, при произвольном 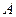 , тогда при
, тогда при 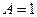 частный случай для плоскости
частный случай для плоскости 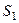 .
.
Один из двух направляющих векторов этой плоскости известен: 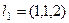 .
Точка .
Точка 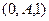 принадлежит прямой, являющейся проекцией.
Точка принадлежит прямой, являющейся проекцией.
Точка 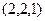 принадлежит той прямой, которая проецируется.
Вектор принадлежит той прямой, которая проецируется.
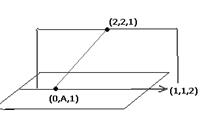
Вектор 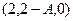 соединяет эти точки. Тогда плоскость, содержащая обе прямые, и проецируемую, и её проекцию (на чертеже эта плоскость расположена вертикально) имеет два образующих вектора: соединяет эти точки. Тогда плоскость, содержащая обе прямые, и проецируемую, и её проекцию (на чертеже эта плоскость расположена вертикально) имеет два образующих вектора: 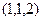 и и 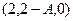 . Их векторное произведение лежит в искомой плоскости (куда проецируется прямая) и является её вторым образующим вектором. . Их векторное произведение лежит в искомой плоскости (куда проецируется прямая) и является её вторым образующим вектором.
|
|
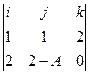 =
= 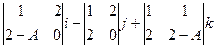 =
= 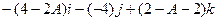 =
=
Итак, второй направляющий вектор плосокости: 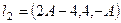 .
.
Теперь через точку 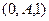 и 2 направляющих
и 2 направляющих 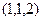 и
и 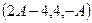 проведём плоскость.
проведём плоскость.
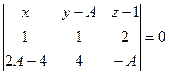
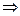
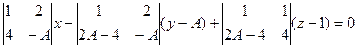
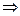
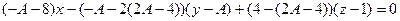
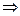
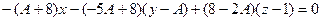
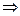
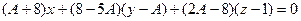
Нормаль к плоскости 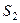 :
: 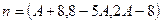 .
.
При 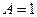 получается нормаль к плоскости
получается нормаль к плоскости 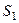 , а именно
, а именно 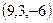 , можно сократить в 3 раза и рассматривать вектор
, можно сократить в 3 раза и рассматривать вектор 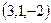 . Осталось узнать, при каком
. Осталось узнать, при каком 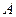 векторы
векторы 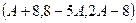 и
и 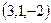 ортогональны между собой.
ортогональны между собой.
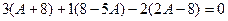
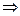
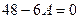
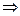
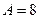 .
.
Ответ. 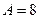 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|