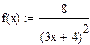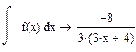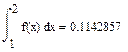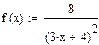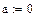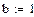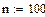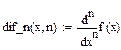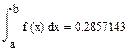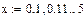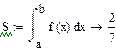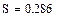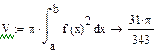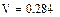Лабораторная работа № 6. Численное интегрирование». Задание к лабораторной работе №6

Лабораторная работа № 6

«Численное интегрирование»

Цель работы: Познакомиться с методами и алгоритмами численного интегрирования, приобрести умения и навыки разработки математического обеспечения на основе программной реализации квадратурных формул.

Рассматриваемые объекты: Определенные интегралы от гладких функций, методы и алгоритмы численного интегрирования, компьютерные инструментальные средства программной реализации алгоритмов и методов, компьютерные средства автоматизации решения вычислительных задач, графические компьютерные средства визуализации результатов работы.

Практическая часть

Вычислить с помощью систем компьютерной математики заданный определенный интеграл и его приложения: длину дуги, объем и площадь тела вращения.
Написать программный модуль для реализации квадратурных формул метода прямоугольников (левых, правых, средних).
Реализовать программно метод трапеций численного интегрирования.
Реализовать алгоритм метода Симпсона с уточнениями для вычисления определенного интеграла.
Вычислить абсолютные и относительные погрешности, выполнить анализ и сравнение результатов, полученных различными методами.
С помощью графических компьютерных средств визуализировать поверхность вращения и криволинейную трапецию (геометрическую интерпретацию определенного интеграла).
Результаты работы оформить в виде отчета.

Задание к лабораторной работе №6

Найти точное (п.1) и приближенное значение интеграла заданной в таблице 1 подынтегральной функции f(x) на отрезке [a, b] по формулам прямоугольников, трапеций, Симпсона (п.2-4) при делении отрезка на 10 и 100 равных частей. Произвести оценку погрешности методов интегрирования и сравнить точность полученных результатов. Выполнить п.5-7 практической части.

Таблица 1

№	Функция	Интервал
1.		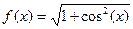[0;3]
2.		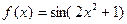[0;1]
3.		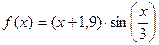[1;2]
4.		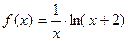[2;3]
5.		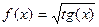[0;0.5]
6.		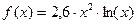[1,2;2,2]
7.		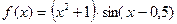[0,5;1,5]
8.		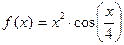[2;3]
9.		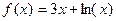[1;2]
10.		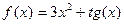[-0,5;0,5]
11.		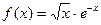[0,1;1,1]
12.		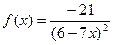[-2;0]
13.		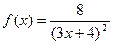[0;1]
14.		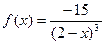[3;5]
15.		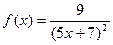[2;3]
16.		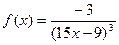[-1;0]
17.		[0;3]
18.		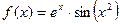[0;5]
19.		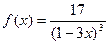[-3;-1]
20.		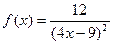[0;1]
21.		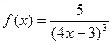[4;5]
22.		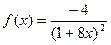[0;3]
23.		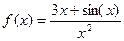[0,1;1,1]
24.		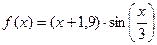[1;2]
25.		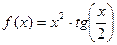[1,5;2,5]
26.		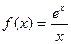[1,7]
27.		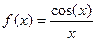[p;p/2]
28.		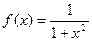[0;1]
29.		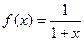[0;9]
30.		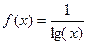[4;10]
31.		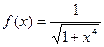[0;6]
32.		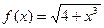[0;3]
33.		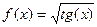[p/3;p/6]
34.		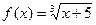[0;8]
35.		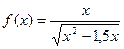[2;5]
36.		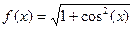[0;p]
37.		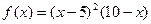[0;10]
38.		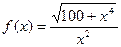[2;4]
39.		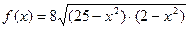[0;2]
40.		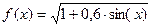[0;p/2]