Обратная матрица

Обратная матрица

Квадратная матрица n–го порядка называется вырожденной, если определитель этой матрицы равен нулю, |A| = 0, и невырожденной, если |A| ≠ 0.
Матрица А^-1 называется обратной матрицей для некоторой квадратной матрицы А, если выполняется соотношение:

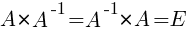
Если матрица А^-1 не вырождена, то существует, и притом единственная, обратная матрица А^-1, равная 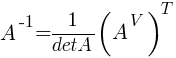, где А^V = A_ij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
1)
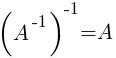
2)
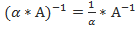
3)
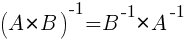
4)

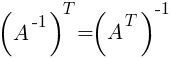
· Алгоритм нахождения А^-1 заключается в следующих пунктах:
1) Находим det A, проверяем det A ≠ 0.
2) Находим M_ij — все миноры матрицы A.
3) Определяем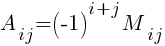
4) Строим матрицу алгебраических дополнений 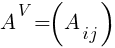и транспонируем: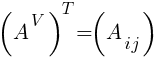
5) Делим каждый элемент матрицы на det A: 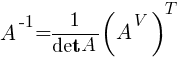Пример 5.

· Элементарные преобразования строк (столбцов) матрицы:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число α ≠ 0;
3) прибавление к элементам строки (столбца) матрицы элементов другой строки (столбца), умноженных на некоторое число.

12 Следующая ⇒