
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
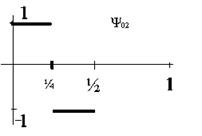
Рисунок 1. Пример локального всплеска.
Лекция 7. Волновой метод (wavelet-метод).
Данный алгоритм является рекурсивным алгоритмом сжатия. На русский язык wavelet переводится как волновое сжатие или как сжатие с использованием всплесков. Этот вид архивации известен довольно давно и напрямую исходит из идеи использования когерентности областей. Ориентирован алгоритм на цветные и черно-белые изображения с плавными переходами. Идеален для картинок типа рентгеновских снимков. Коэффициент сжатия задается и варьируется в пределах 5-100. При попытке задать больший коэффициент на резких границах, особенно проходящих по диагонали, проявляется “лестничный эффект” — ступеньки разной яркости размером в несколько пикселов.
Обоснование метода заключается в использовании локального всплеска (см. рис. 1) вместо глобально-периодических функций, т.е. таких функций 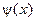 , что:
, что:
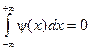 и
и 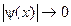 , при
, при 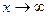 .
.
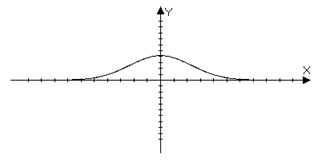
Рисунок 1. Пример локального всплеска.
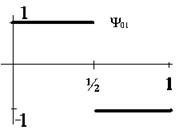
Рассмотрим пример таких функций - систему Хаара. В общем виде она записывается так:
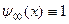

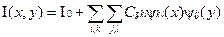 - общий вид обратного
- общий вид обратного
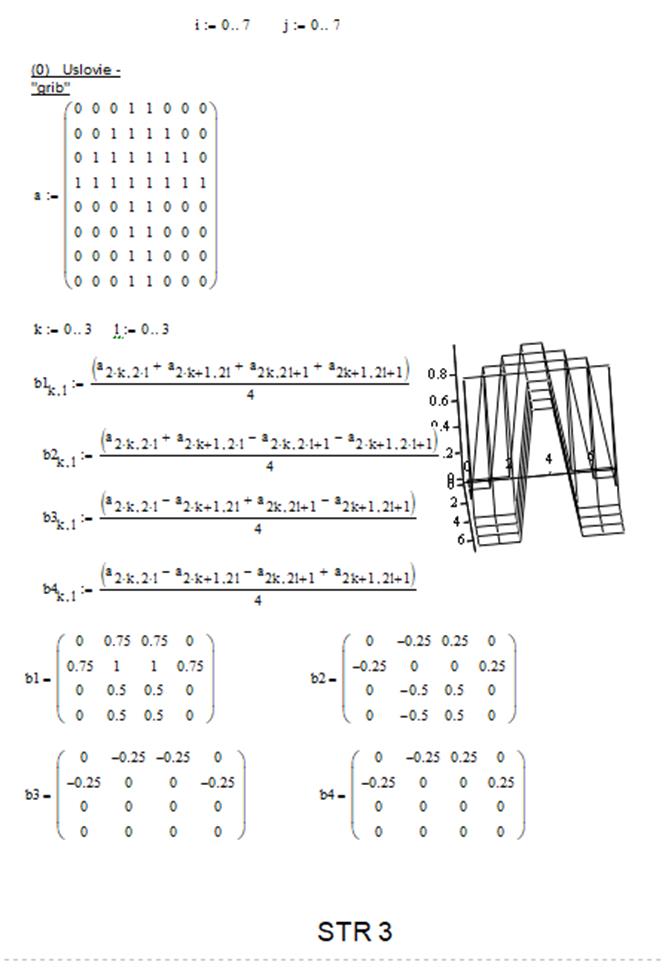
Если преобразование применяется к строке то так (здесь рассматриваем функцию 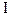 , которая определена на отрезке от 0 до 1, который разбит на
, которая определена на отрезке от 0 до 1, который разбит на 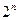 частей, см. рис. 2):
частей, см. рис. 2):
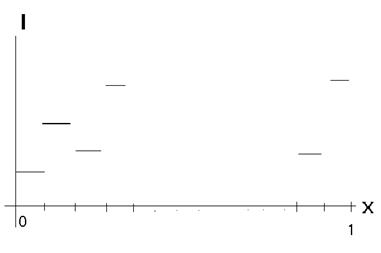
Рисунок 2. Строка изображения
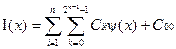
Получается, что мы берём на каждом шаге некоторое среднее значение функции в точке.
Пусть 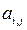 - величина яркости точки (i,j). Идея алгоритма заключается в том, что мы сохраняем в файл разницу — число между средними значениями соседних блоков в изображении, которая обычно принимает значения, близкие к 0. Нетрудно видеть, что расчетные формулы в случае двухмерного изображения будут иметь вид:
- величина яркости точки (i,j). Идея алгоритма заключается в том, что мы сохраняем в файл разницу — число между средними значениями соседних блоков в изображении, которая обычно принимает значения, близкие к 0. Нетрудно видеть, что расчетные формулы в случае двухмерного изображения будут иметь вид:
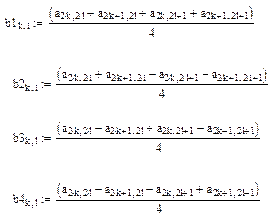
Используя эти формулы, например, для изображения 512х512 пикселов получим после первого преобразования 4 матрицы размером 256х256 элементов.
В первой, как легко догадаться, будет храниться уменьшенная копия изображения. Во второй — усредненные разности пар значений пикселов по горизонтали. В третьей — усредненные разности пар значений пикселов по вертикали. В четвертой — усредненные разности значений пикселов по диагонали. По аналогии с двумерным случаем мы можем повторить наше преобразование и получить вместо первой матрицы 4 матрицы размером 128х128. Повторив наше преобразование в третий раз, мы получим в итоге: 4 матрицы 64х64, 3 матрицы 128х128 и 3 матрицы 256х256. На практике при записи в файл, значениями, получаемыми в последней строке (), обычно пренебрегают (сразу получая выигрыш примерно на треть размера файла — 1- 1/4 - 1/16 - 1/64...).
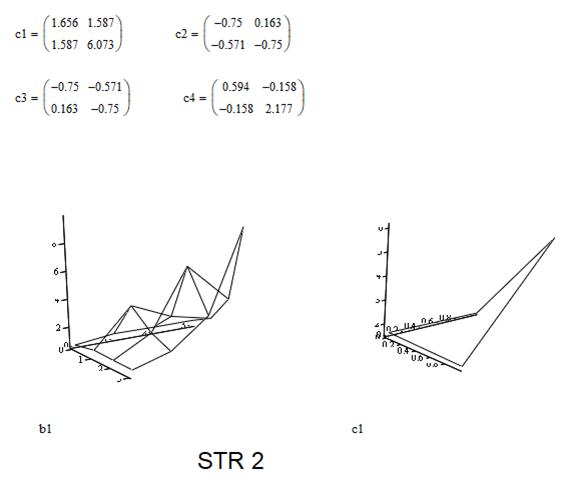
К достоинствам этого алгоритма можно отнести то, что он очень легко позволяет реализовать возможность постепенного “проявления” изображения при передаче изображения по сети. Кроме того, поскольку в начале изображения мы фактически храним его уменьшенную копию, упрощается показ “огрубленного” изображения по заголовку.
В отличие от JPEG и фрактального алгоритма, которые будут описаны ниже, данный метод не оперирует блоками, например, 8х8 пикселов. Точнее, мы оперируем блоками 2х2, 4х4, 8х8 и т.д. Однако за счет того, что коэффициенты для этих блоков мы сохраняем независимо, мы можем достаточно легко избежать дробления изображения на “мозаичные” квадраты.
Следующие далее листы необходимо распечатать, вклеить в тетрадь и захватить с собой на практику!

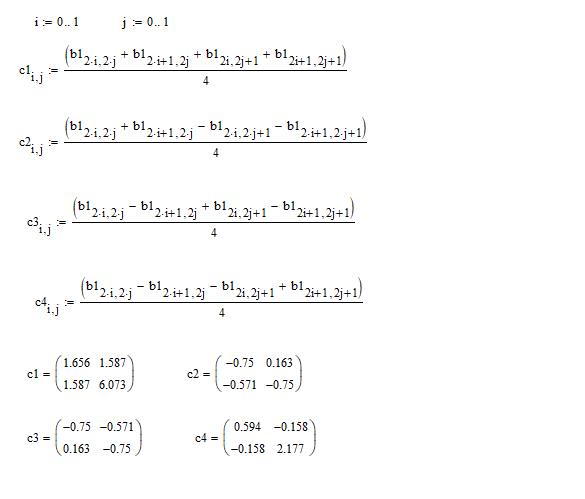


|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|