Горизонтальная съемка

Горизонтальная съемка

Горизонтальная съемка местности в простейшем варианте выполняется с помощью теодолита и рулетки. Съемочное обоснование обычно создают проложением теодолитных ходов. Если участок съемки имеет вытянутую форму, то теодолитный ход прокладывают по его оси; при этом отдельные пункты съемочного обоснования можно определять из геодезических засечек. Если участок имеет овальную форму, то прокладывают замкнутый ход по его границе; внутри участка можно проложить диагональные ходы.

При горизонтальной съемке положение отдельных точек определяют относительно пунктов съемочного обоснования и линий, соединяющих их, применяя:

· способ засечек ( угловых, линейных, комбинированных );

· полярный способ;

· способ перпендикуляров;

· способ створов.

Широко также применяется способ обмеров зданий и сооружений и расстояний между ними с помощью рулетки.

Способ засечек. При угловой засечке положение точки 1 определяют относительно двух пунктов съемочного обоснования А и В с помощью двух измеренных горизонтальных углов α1 и β1. Положение другой точки – точки 2 определяют, измеряя два других угла α2 и β2 (рис.7.3). Результаты измерений записывают в журнал.

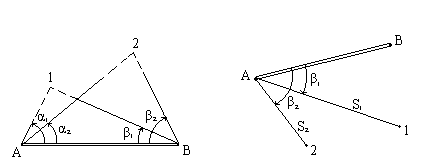
Рис.7.3 Рис.7.4

При построении плана при точках А и В с помощью транспортира строят углы α1 и β1 и в пересечении линий получают изображение точки 1 на плане. Аналогично находят на плане положение точки 2.

Если расстояние до точки 1 не превышает длины рулетки, положение точки 1 определяют линейной засечкой, при которой измеряют расстояния А – 1 и В – 1 ; при построении плана из точки А проводят дугу радиусом, равным расстоянию А – 1 в масштабе плана, а из точки В – радиусом, равным расстоянию В – 1 в масштабе плана. Точка пересечения этих дуг является изображением точки 1 на плане.

Точность измерения горизонтальных углов при угловой засечке определяется точностью их построения на плане транспортиром,т.е. порядка 10′ – 15′. Допустимую ошибку измерения расстояний при линейной засечке рассчитывают по формуле:

ms = 0,3 мм * М,

где М – знаменатель масштаба съемки.

Полярный способ. Полярный способ съемки – это реализация полярной системы координат. Теодолит устанавливают на пункте съемочного обоснования А, принимая его за начало ( полюс ) местной полярной системы координат. Полярная ось совмещается с направлением на другой пункт съемочного обоснования В. Затем измеряют горизонтальный угол β1, образованный направлением АВ и направлением на снимаемую точку 1, и расстояние S1 от точки А до точки 1 (рис.7.4). При построении плана положение точки 1 получают, откладывая на стороне угла β1, построенного транспортиром, расстояние S1 в масштабе плана.

Рассчитаем среднюю квадратическую ошибку измерения углов и расстояний при полярном способе съемки, если ошибка положения точки 1 задана и равна Мp.

В полярной системе координат ошибка положение точки выражается формулой:

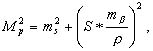(7.1)

где mβ – ошибка измерения угла β; ms – ошибка измерения полярного расстояния.

По принципу равных влияний имеем:

m2s = ( S * mβ/ 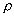)2 = M2 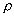/2, (7.2)

откуда

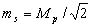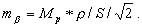и (7.3)

Пусть масштаб съемки 1:М=1:2 000, тогда Мp=0.5 мм * 2 000=1 м. При S=100 м вычисления по формулам (7.3) дают mβ=24′, ms =0.7м, ms/S = 1/150.

Способ перпендикуляров. Способ перпендикуляров является реализацией обычной прямоугольной системы координат. Пусть линия АВ – одна из сторон теодолитного хода. Примем ее за ось l, начало координат совместим с пунктом А; ось d расположим перпендикулярно линии АВ. Положение точки 1 определяется двумя перпендикулярами l1 и d1 (рис.7.5), длины которых измеряют мерной лентой или рулеткой.

Рис.7.5

Для построения прямого угла β можно применять теодолит или эккер; иногда угол β = 90 можно построить на глаз. Положение точки 1 на плане получают после выполнения трех операций: откладывания вдоль линии АВ длины перпендикуляра l1, построения угла β =90 c помощью транспортира, откладывания на стороне угла β длины второго перпендикуляра d1.

Съемка других точек и определение их положения на плане выполняются в таком же порядке.

Ошибка положения точки Мp в способе перпендикуляров складывается из ошибки измерения перпендикуляра l, ошибки построения (или измерения) угла β = 90 o и ошибки измерения перпендикуляра d:

М2p = m^2l + mβ ^2/ 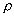^2 * d^2 + m^2d. (7.4)

По принципу равных влияний полагаем:

m^2l = m β^2/ 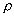^2 * d^2 = m^2d = M^2p/3. (7.5)

При Мp = 0.5 мм на плане получим 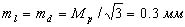в масштабе плана. Приняв ошибку построения угла mβ= 30′, рассчитаем допустимую длину перпендикуляра d:

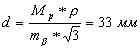
в масштабе плана при относительной ошибке его измерения:

md / d = 0.33 мм / 33 м = 1/110.

Для плана масштаба 1 : 2 000 расчетная длина перпендикуляра d получается 66 м, а для масштаба 1 : 500 – d = 16 м. В Инструкции эти величины заданы 60 м и 20 м соответственно.

Разумеется, при другом значении ошибки mβ допустимая длина перпендикуляра d будет другой. Например, строя угол β = 90 “на глаз” (mβ = 1) , получим d = 16 мм в масштабе плана.

При горизонтальной съемке результаты измерений углов и линий записывают в журнал. Кроме того, прямо в поле составляют схематический чертеж местности – абрис, на котором показывают все пункты съемочного обоснования, контуры, ситуацию местности, записывают результаты измерений, делают пояснительные записи.

По материалам съемки составляют и вычерчивают план участка.

Теория и устройство эккера. Эккер – прибор для построения на местности прямых углов. Эккеры бывают зеркальные и призменные. Зеркальный эккер состоит из трехгранной коробки, одна из боковых граней которой открыта (рис.7.6). К двум другим граням с внутренней стороны прикреплены зеркала. Над зеркалами вырезаны окошки. Внизу эккера имеется крючок для отвеса.

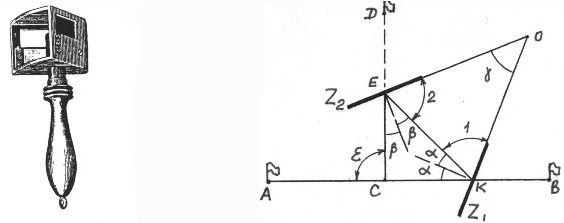
Рис.7.6 Рис.7.7

Пусть эккер установлен на линии АВ (рис.7.7). Луч от вехи А попадает в зеркало Z1, отражается от него, падает на зеркало Z2, отражается от него и попадает в глаз наблюдателя, составляя со своим первоначальным направлением угол ε. Теория эккера заключается в выводе формулы ε = ε (γ), где γ – угол между зеркалами.

Обозначим : α – угол падения и угол отражения на зеркале Z1, β – угол падения и угол отражения на зеркале Z2.

Угол ε является внешним углом треугольника СЕК, поэтому:

ε = 2 * α + 2 * β = 2 * (α + β ). (7.6)

В треугольнике ЕОК:

γ = 180 – (

Но

поэтому

γ = α + β.

Отсюда

ε = 2 * γ,

или

γ = ε/2. (7.7)

Для того, чтобы луч составлял со своим прежним направлением угол β = 90, нужно, чтобы угол между зеркалами был равен 45.

Глаз видит изображение вехи А в зеркале Z2 в направлении СЕ, перпендикулярном направлению АВ, а в окошко над зеркалом видно веху D, которую помощник переставляет по команде наблюдателя. Как только веха D будет находиться на линии CE, ее закрепляют.

Если вехи закреплены, то с помощью эккера можно найти на линии АВ точку С, чтобы линия DC была перпендикулярна АВ; другими словами, можно найти основание перпендикуляра, опущенного из точки D на линию АВ. Взяв в руки эккер, перемещаются по линии АВ, пока изображение вехи А в зеркале Z2 не совпадает с направлением CD. Затем при помощи отвеса намечают на земле точку С.

Поверка эккера. Угол между зеркалами должен быть равен 45. Стоя в точке С, строят прямой угол, наблюдая веху А, закрепляют прямой угол первой вехой. Затем, стоя по-прежнему в точке С, строят прямой угол, наблюдая веху В, закрепляют прямой угол второй вехой. Если вехи оказались рядом, условие эккера выполняется. В противном случае намечают среднее положение, ставят веху в эту точку и юстировочными винтами зеркал изменяют угол между зеркалами до тех пор, пока изображение вехи А или В не совпадет с направлением CD. После этого поверку повторяют. Эккер считается исправным, если угол γ отличается от 45 не больше, чем на 2.5′, тогда ошибка построения угла β = 90 будет не больше 5′.