Урок 2. ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ

Урок 2. ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ

Цели: доказать признаки равенства прямоугольных треугольников и показать, как они применяются при решении задач.

I. Повторение изученного материала.

1. Сформулировать свойства прямоугольных треугольников.

2. Вспомнить признаки равенства треугольников.

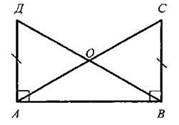
3. Решить задачу: гипотенузы ВД и АС прямоугольных треугольников АВД и ABC с общим катетом АВ и с равными катетами АД и ВС пересекаются в точке О (см. рис.).

Докажите, что треугольник АОВ равнобедренный.

II. Изучение нового материала.

1. Учащиеся самостоятельно (устно), используя признаки равенства треугольников, доказывают признаки равенства прямоугольных треугольников по двум катетам, по катету и прилежащему острому углу, по гипотенузе и острому углу (учитель держит перед классом два равных прямоугольных треугольника и задает наводящие вопросы).

2. Доказательство признака равенства прямоугольных треугольников по гипотенузе и острому углу (устно) по моделям равных прямоугольных треугольников.

3. Доказательство признака равенства прямоугольных треугольников по гипотенузе и катету проводит сам учитель (рис. 133 учебника), так как доказательство этого признака требует дополнительных построений и непростых логических рассуждений.

III. Закрепление изученного материала.

1. Решить задачу № 261 на доске и в тетрадях.

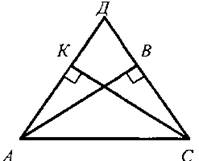
Дано: ΔАДС; АД = ДС; АВ и СК - высоты.

Доказать: АВ = СК.

Доказательство:

По условию АВ ⊥ ДС и СК ⊥ АД, тогда ΔАВС и ΔАКС - прямоугольные; в них АС - общая гипотенуза и ∠KAC = ∠ВСА, так как по условию ΔАДС равнобедренный.

Значит, ΔАВС = ΔСКА (по гипотенузе и острому углу).

Тогда АВ = СК.

2. Учащиеся самостоятельно формулируют и доказывают признак равенства прямоугольных треугольников по катету и противолежащему углу (задача № 268).

3. Решить задачу № 269 на доске и в тетрадях.

Указание: при решении задачи применить вывод задачи № 268 - признак равенства прямоугольных треугольников по катету и противолежащему углу.

IV. Итоги урока.

Домашнее задание: изучить п. 36; ответить на вопросы 12-13 на с. 88-89; решить задачи № 262, 264.