Тема: Признаки равенства прямоугольных треугольников

Тема: Признаки равенства прямоугольных треугольников

Урок 3. РЕШЕНИЕ ЗАДАЧ

Цели: научить применять признаки равенства прямоугольных треугольников и их свойства при решении задач; вырабатывать умение решать задачи; учить логически мыслить.

I. Устная работа.

1. Сформулировать свойства прямоугольных треугольников.

2. Сформулировать признаки равенства прямоугольных треугольников.

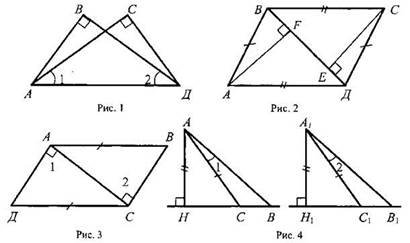
3. Устно решить задачи по готовым чертежам:

1) На рисунке 1 ∠5 = ∠C = 90°; ∠1 = ∠2. Докажите, что АВ = СД.

2) На рисунке 2 АВ = СД; ВС = АД, ∠AFB = ∠СЕД = 90°. Докажите, что BF = ЕД; AF = ЕС.

3) На рисунке 3 ∠1 = ∠2 = 90°, АВ = ДС. Докажите, что ВС = АД.

4) На рисунке 4 АН и А1Н1 - высоты треугольников ABC и А1В1С1; АС = А1С1; ∠1 = ∠2; AH = A1H1.

Докажите, что ΔАВС = ΔА1В1С1.

II. Решение задач.

1. Решить задачу № 263 в тетрадях.

2. Решить задачу № 267 в тетрадях.

Указание: при доказательстве применить признак равенства прямоугольных треугольников по гипотенузе и катету.

III. Самостоятельная работа (проверочного характера) (20 мин).

Вариант I

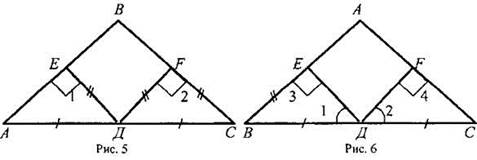
1. На рисунке 5 АД = ДС; ЕД = ДF; ∠1 = ∠2 = 90°. Докажите, что треугольник ABC равнобедренный.

2. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 18 см. Найдите гипотенузу и меньший катет.

Вариант II

1. На рисунке 6 ∠1 = ∠2, ∠3 = ∠4 = 90°; ВД = ДС. Докажите, что треугольник ABC равнобедренный.

2. Один из острых углов прямоугольного треугольника в два раза меньше другого, а разность гипотенузы и меньшего катета равна 15 см. Найдите гипотенузу и меньший катет.

Вариант III (для более подготовленных учащихся)

1. Через середину отрезка АВ проведена прямая а. Из точек А и В к прямой а проведены перпендикуляры АС и ВД. Докажите, что АС = ВД.

2. В прямоугольном треугольнике СДЕ с прямым углом Е проведена высота EF. Найдите CF и РД, если СД = 18 см, а ∠ДСЕ = 30°.

Вариант IV (для более подготовленных учащихся)

1. Из точки М биссектрисы неразвернутого угла О проведены перпендикуляры МА и MB к сторонам этого угла. Докажите, что МА = MB.

2. В прямоугольном треугольнике ABC с гипотенузой АВ и ∠A = 60° проведена высота СН. Найдите ВН, если АН = 6 см.

IV. Итоги урока.

V. Домашнее задание: повторить пункты 31-36; прочитать п. 37 можно сделать презентацию и получить еще оценку; решить № 258, 265.