Kл= ; Δл=100(Кл-1). Мс(t)= , миль

РШ= φ2 - φ1 РД= λ2 - λ1

φ2 = φ1 + РШ λ2 = λ1 + РД

помня, что все эти формулы являются алгебраическими и требуют подстановки в правую часть равенств значений с принятыми в навигации знаками. Решение каждой задачи подтверждается пояснительными чертежами на сфере и графике. Особенно внимательно к вычислению РД следует отнестись в тех случаях, когда судно пересекает меридиан 180°, т.е. переходит из восточного полушария в западное или наоборот. В этом случае необходимо помнить, что разностью долгот считается меньшая из двух дуг экватора, а поэтому если РД какого-либо наименования получается больше 180°, то брать ее следует как дополнение полученной величины до 360° и приписывать ей обратное наименование.

При решении задач на расчет дальности видимости предмета в море следует пользоваться таблицами 2.1, 2.3, номограммой 2.4 МТ-2000.

На морских навигационных картах магнитное склонение дается на определенный год, и поэтому возникает необходимость приведения склонения к текущему году плавания. Основанием для этого служит указание в заголовке карты или в местах расположения магнитного склонения, о годовом изменении склонения. Зная склонение в районе плавания и его изменения, а также количество лет, прошедших от года, к которому приведено склонение на карте, до года плавания, можно рассчитать как изменение склонения, так и само склонение для данного года.

В румбовой системе весь горизонт делится на 32 румба (1 румб=11,25°). Эта система в качестве основной применялась в эпоху парусного флота, когда высокая точность в отсчетах направлений не требовалось. Однако деление истинного горизонта на румбы не потеряло своего значения и в настоящее время, так как направление ветра и волнения указываются и теперь в румбах. Перевод направлений из одной системы в другую производится логическим путем, например 5-ый румб четверти NW=NWtW (румбовая)=56,25° NW (четвертная)=303,75° (круговая). Правильность перевода можно проверить данными из таблицы 5.13 МТ-2000.

При решении задач на перевод и исправление направлений по формулам необходимо помнить, что курсы и пеленги отрицательными быть не могут, и если при решении уменьшаемое число меньше вычитаемого, то к уменьшаемому добавляется 360°. Если результат решения получается больше 360°, то 360° надо отбросить. Решение задач поясняется графическим чертежом.

Лаг, как и всякий прибор, имеет погрешности в измерении скорости и пройденного расстояния, поэтому каждый лаг имеет поправку, которая выражается либо в процентах Δл, либо в виде коэффициента Кл. Расчет их производится по формулам:

Δл%= 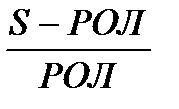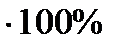; Кл=1+

где S – истинное расстояние, пройденное судном за определенное время, мили.

РОЛ – разность показаний лага за то же время.

Расчет Δл и Кл (задача №16) следует вести с точностью 0,5% и 0,01 соответственно. При определении Vл, Δл и Кл на мерной линии (задача №19) при наличии течения, имеющего неизменные направление и скорость, необходимо делать два пробега по взаимно противоположным направлениям. В этом случае осреднением результатов наблюдений на двух пробегах исключают влияние течения на определяемую скорость хода, т.е. получают скорость судна относительно воды. Расчет производится по формулам:

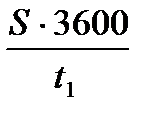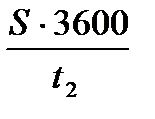V1= ; V2= ; Vл=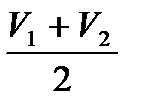

где Vл – скорость судна относительно воды,

(V1 - скорость судна на 1 пробеге )

(S – длина мерной линии)

(t1 – время 1-го пробега)

(V2 – скорость судна на 2 пробеге)

(t2 – время 2-го пробега)

или по формуле:

Vл=S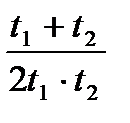

Далее рассчитывается: 1) Пройденное судно расстояние относительно воды

Sл=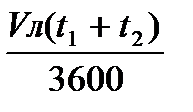

2) Суммарная разность отсчетов лага РОЛ=РОЛ1+РОЛ2.

3) Рассчитывается Кл и Δл

Kл= ; Δл=100(Кл-1)

Задача №17 решается графически, желательно на миллиметровой бумаге, карандашом в удобном масштабе так, чтобы искомые данные можно было определить с точностью до 1° и до 0,2 узла. Если в условии задан КК, то это прямая задача на совместный учет дрейфа и течения, если ПУс – обратная. Методика графического решения прямой и обратной задач изложена достаточно подробно в учебниках по навигации.

Элементы, характеризующие движение судна и учитываемые при счислении (истинный курс и проходимое судном расстояние), известны с некоторыми погрешностями. Поэтому, как бы точно ни решались задачи по учету этого движения, получаемые счислимые места судна всегда следует рассматривать как приближенные и погрешности этих мест будут тем больше, чем большее время ведется счисление. Точность счислимого места судна при графическом счислении определяется следующими факторами:

mпу – средней квадратической погрешностью (СКП) путевого угла,

mΔл% - средней квадратической погрешностью поправки лага:

Мс(t) – радиальная средняя квадратическая погрешность, определяется по формуле

Мс(t)= , миль

Задачу №21 необходимо решить с использованием номограмм 4.10.1 и 4.10.2 МТ-2000. Обе номограммы вычислены по формулам:

⇐ Предыдущая 123 4 Следующая ⇒