Рис. 23. К расчету прочности сечения нижнего пояса безраскосной фермы

Рис. 23. К расчету прочности сечения нижнего пояса безраскосной фермы

Расчет прочности выполняем согласно п. 3.70[7] c уточнением для предва- рительно напряженного элемента. Вычисляем эксцентриситет продольной силы е0 = М / N = 8,265 / 638,81 = 0,0129 м = 12,9 мм. Вычисляем эксцентриситет е' = е0 + h / 2 − а'р = 12,9 + 220 / 2 − 50 = 72,9 мм.

Так как е’ = 72,9 мм < h0 − а'р = 170 − 50 = 120 мм, то продольная сила

приложена между равнодействующими усилий в арматуре Sp и S'р и требуемую площадь сечения симметричной арматуры определяем по формуле (3.138) [7]:

Asp = A'sp =Ne' /[γs3 Rs(h0 − а'р)] = 638,81·103·72,9/[1,1·1050(170 − 50)] =336 мм2;

где γs3= 1,1 (см. п. 3.9 [9]).

Принимаем по 8Ø8Вр1200, Asp,fact = 402 мм2);

Выполняем расчет прочности наклонного сечения нижнего пояса фермы в наиболее загруженном элементе между расчетными 10 и 11 (см. рис. 22 и 24) в соответствии с п. 3,34 [9] c учетом указаний п. 3.71 [7] на действие по- перечной силы Q = 37,19 кН.

Расчет выполняем с учетом наличия продольной растягивающей силы N =

=586,0 кН и усилия обжатия от напрягаемой арматуры, расположенной в наи- более растянутой зоне Р=σsp2Asp=630·402=253260 H=253,26 кН , где σsp2 =

=0,7σsp= 0,7·900 = 630 МПа. (Коэффициент 0,7 учитывает, что полные потери

предварительного напряжения приблизительно будут равны 0,3σsp).

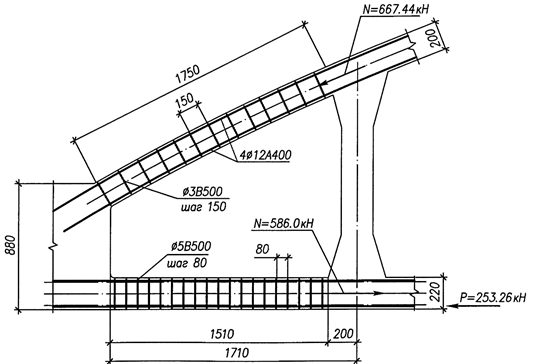
Рис. 24. К расчету прочности наклонных сечений поясов безраскосной фермы

Примем поперечное армирование по конструктивным соображениям в ви- де замкнутых двухветвевых хомутов из арматуры диаметром 5 мм класса В500 с шагом sw = 80 мм < h0/2 = 170/2 = 85 мм (Asw=2·19,6= 39,2 мм2, Rsw = 300 МПа). Определим коэффициент φnt по формуле (3.143) [7], принимая А= bh =

=240·220 = 52800 мм2:

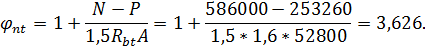
Вычисляем величины Mb и qsw :

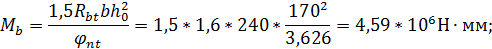
qsw = Rsw Asw / sw = 300·39,2/80 = 147,0 Н/мм.

Поскольку qsw > 0,25Rbtb/ φnt =0,25·1,6·240/3,626=26,47 Н / мм, то Mb не корректируем.

Находим Qb,min = 0,5Rbt bh0/φnt = 0,5·1,6·240·170/3,626 = 9002 H= 9,002 кН.

Так как поперечная сила не изменяется по длине элемента, принимаем длину проекции наклонного сечения равной длине элемента с =1510 мм > 3h0=

= 3·170 = 510 мм, следовательно, с = 510 мм. Тогда с0 = с = 510 мм > 2h0 =

=2·170 = 340 мм, т.е. с0 = 340 мм.

Поскольку Qb=Mb / с = 4,59·106 / 510=8053 Н = 8,053 кН <Qb,min =9,002 кН, принимаем Qb = 9,002 кН; Qw=0,75qsw с0 =0,75·147,0·0,34 = 37,485 кН.

Таким образом, предельная несущая способность нижнего пояса фермы в наиболее опасном наклонном сечении будет равна:

Q = Qb + Qsw= 9,002+37,485 = 46,5 кН > Q = 37,19 кН,

следовательно прочность нижнего пояса фермы на действие поперечной силы обеспечена. Требования п. 3.36[9] также выполняются, поскольку:

sw,max=

R bh / Q

bt 0 max

= 1,6·240·1702

/ (37,19·103) = 298 мм > sw= 80 мм.

Расчет элементов верхнего пояса фермы. Для сечения 6 имеем усилия от расчетных нагрузок: N = 669,37 кН; М = 37,77 кН∙м. Усилия от постоянной и длительной части снеговой нагрузки вычислим по формулам:

Nl=Ng + 0,7( N – Ng) = 511,95+0,7(669,37 – 511,95) = 622,14 кН,

Ml=Mg + 0,7( M – Mg) = 28,89+0,7(37,77 – 28,89) = 35,11 кН·м,

где коэффициент 0,7 учитывает долю длительной составляющей снеговой нагрузки.

Корректируем значения изгибающих моментов:

М = 37,77 ·0,7 = 26,44 кН·м , Ml= 35,11·0,7 = 24,57 кН·м;

где 0,7 – коэффициент, учитывающий перераспределение изгибающих моментов в верхнем поясе фермы.

Геометрические размеры сечения и расположение арматуры дано на рис.25, а. Расчетная длина элемента в плоскости фермы (см. табл. IV.10 при- ложения IV), при эксцентриситете е0 = M/N = 26,44/669,37 =0,0395 м =39,5 мм >

>h/8 = 200/8=25 мм, будет равна l0 = 0,8l =0,8·3,13 = 2,504 м.

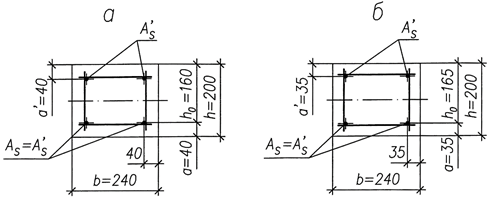
Рис. 25. К расчету прочности сечения верхнего пояса и стоек безраскосной фермы: а – сечение верхнего пояса; б – сечение стойки

Находим случайный эксцентриситет: ea=h/30 = 6,7 мм; еа=l/600 =

=3130/600 = 5,2 мм; еа=10 мм; принимаем наибольшее значение еа = 10 мм.

Поскольку е0 = 39,4 мм > еа = 10 мм, то оставляем для расчета е0 = 39,4 мм. Так как l0/h = 2504/200 = 12,52 > 4, то расчет прочности ведем с учетом влияния прогиба на значение эксцентриситета продольной силы.

Согласно п. 3.54[7] определяем коэффициент η. Находим:

h - a M = M + N 0

1 2

= 26,44 + 669,37 0,16 - 0,04 = 66,6

кН·м;

M1l

= Ml

+ Nl

h0 - a

= 24,57 + 622,14 0,16 - 0,04 = 61,9

кН·м;

φl = 1 + M1l / M1 = 1 + 61,9/66,6 = 1,929.

Так как е0 / h = 39,5 / 200 = 0,197 > 0,15, принимаем δе = 0,197.

В первом приближении принимаем μ = 0,010, находим μα = 0,010·5,263=

=0,05263, где α =Es /Eb = 200000/38000 = 5,263.

По формуле (3.89)[7] определим жесткость D:

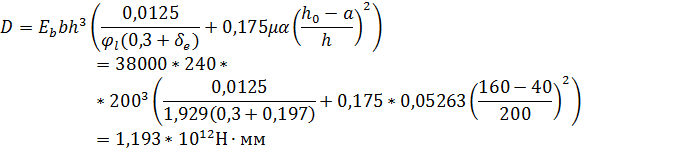
Отсюда:

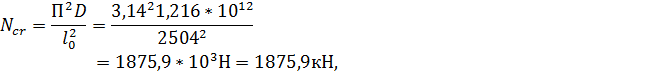
тогда:

Мη = Мη = 26,44·1,555 = 41,11 кН·м.

Необходимую площадь сечения симметричной арматуры определим со- гласно п.3.57[7]. Для этого вычислим значения:

α= N

Rbbh0

= 669,37 ×10 27,5 × 240 ×160

= 0,6339;

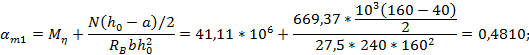
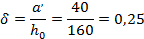
Так как αn= 0,6339 > ξR = 0,533 , то требуемое количество симметричной арматуры определим по формуле (3.94)[7], для чего необходимо вычислить значения ξ1 αs и ξ :

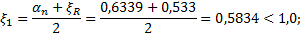
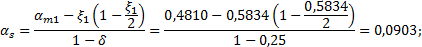
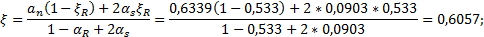
Тогда получим:

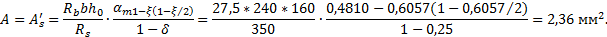
Принимаем S и S’ по 2Ø14А400 с As = As

= 308 мм , тогда:

μ = As

+ As

= 2 × 308 240 × 200

= 0,0128,

что близко к предварительно принятому значению μ = 0,010 и не требует второго приближения.

Элемент 1 – 2 – 3, сечение наклонное к продольной оси Q1 = 9,74 кН; Qmax = Q3 = 52,74 кН; N = 667,44 кН. Длина элемента l1–3 = 1,75 м (см. рис. 24).

Расчет выполняем согласно пп. 3.41 и 3.52 [7]. Находим коэффициент φn2

по формуле (3.84) [7]:

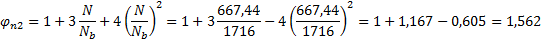
где Nb = 1,3RbA = 1,3·27,5·240·200=1716·103 Н = 1716 кН.

Проверим условие (3.64) [7]: 2,5Rbtbh0 = 2,5·1,6·240·160 = 153,6·103 Н =

=153,6 кН > Qmax = 52,74 кН, т. е. условие выполняется.

Проверим условие (3.65) [7], принимая максимальное значение с =

=cmax = 3h0 = 3·160 = 480 мм и значение поперечной силы в конце наклонного сечения Q = Q3 – c(Q3 – Q1)/l1–3 = 52,74 – 0,48(52,74 – 9,74)/1,75 = 40,95 кН,

тогда получим:

n 2 bt 0

1,5φ R bh2 / c = 1,5·1,562·1,6·240·1602

/ 480 =

=47,98 ·103 Н = 47,98 кН > Q= 40,95 кН,

т. е. и второе условие выполняется. Следовательно, прочность наклонного сечения обеспечена без поперечной арматуры.

С учетом конструктивных требований для сжатых элементов принимаем поперечную арматуру для верхнего пояса фермы диаметром 4 мм класса Вр500 с шагом 200 мм < 15d = 15·14 = 210 мм.

Расчет стоек фермы. Стойки безраскосной фермы рассчитываются на не- благоприятные сочетания усилий N и М. Для примера рассмотрим порядок оп- ределения площади сечения продольной арматуры в сжато–изогнутой стойке 16 – 17 (см. рис. 22 и 25, б), N=25,89 кН; М = |Мmax| = 26,81 кН·м.

Расчетная длина l0 = 0,8l = 0,8 ·1,590 = 1,272 м. Находим случайный экс-

центриситет: ea=h/30 =200/30 = 6,7 мм; еа=l/600 = 1590/600 =2,65 мм; еа=10 мм; принимаем наибольшее значение еа = 10 мм.

Поскольку е0 = M/N=26,81/25,89=1,036 м = 1036 мм > еа = 10 мм, то ос- тавляем для расчета е0 = 1036 мм. Так как l0/h = 1272/200 = 6,36 > 4, то расчет прочности ведем с учетом влияния прогиба на значение эксцентриситета про- дольной силы.

Согласно п. 3.54[7] определяем коэффициент η при φl = 1,929. Так как е0 / h = 1036 / 200 = 5,18 > 0,15, принимаем δе = 5,18.

В первом приближении принимаем μ = 0,025, находим

μα = 0,025·5,263= 0,1316, где α =Es /Eb = 200000/38000 = 5,263.

Выполнив вычисления формулам (3.89), (3.87) и (3.89) [7] (см. расчет эле- ментов верхнего пояса фермы) получим следующие значения параметров:

D = 7,962·1011 Н·мм2 , Ncr = 4852 кН, η = 1,005,

тогда:

Мη = Мη = 26,81·1,005 = 26,94 кН·м.

Необходимую площадь сечения симметричной арматуры определим со- гласно п.3.57[7]. Для этого вычислим значения:

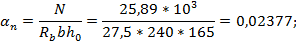
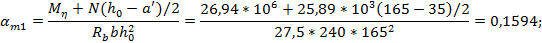
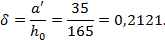
Так как αn= 0,02377 < ξR = 0,533 , то требуемое количество симметричной арматуры определим по формуле (3.93)[7]:

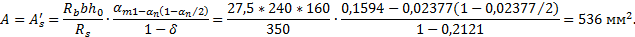
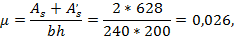
Принимаем As=A's= 628 мм2 (2Ø20A400), при этом

что близко к предварительно принятому значению μ = 0,025 и не требует второго приближения.

Аналогично рассчитываются и конструируются остальные стойки фермы. По заданию требуется выполнить еще расчет и конструирование опорного узла фермы, для чего следует руководствоваться примером расчета опорного узла сегментной фермы, приведенным в п. 2.2.

Пример заполнения контрольного талона к расчету стропильной конструкции с обозначением контролируемых параметров дан на рисунке 12.

а ========================================================================================================================

ПГС 4 курс П11 гр.I Kод Bерхний пояс Нижний пояс Cт.или р.Oп.узел G(МПа) R(МПа) Kонтр. I Соколов С.Н. Iзадания S1(n.ф) S2(n.ф) ф.sw1 Sp1(n.ф) Sp2(n.ф) ф.sw2 S3(n.ф) ф.sw3 sp bp сумма I Cрок сдачи информацииI : : : : : : : : : : : I по 3 этапу до 90310I 107.03 2.10 2.10 4.150 3.22 2.22 4.120 2.10 8.290 500 25 660.33 I

=====================I------------------------------------------------------------------------------------------------------------------------------------------- I

Пояснения к заполнению контрольного талона:

S1(n.ф) S2(n.ф) – количество и диаметры продольной рабочей арматуры верхнего пояса (например 2Ø12 следует записать 2.12);

ф.sw1 – диаметр (целая часть) и шаг (дробная часть) поперечной арматуры в элементах верхнего пояса, мм;

Sp1(n.ф) Sp2(n.ф) – количество и диаметры напрягаемой арматуры нижнего пояса;

ф.sw2 – диаметр и шаг поперечной арматуры в элементах нижнего пояса;

S3(n.ф) – количество и диаметр продольной рабочей арматуры у наиболее нагруженной грани сечений стоек или раскосов;

ф.sw3 – диаметр и шаг поперечной арматуры в опорной части (узле) стропильной конструкции;

G – величина начального предварительного напряжения арматуры, МПа;

R – передаточная прочность бетона, МПа.

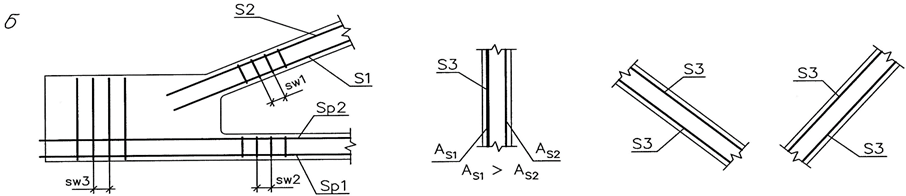
Рис. 12. К автоматизированной проверке расчета и конструирования стропильной конструкции:а – заполненный контрольный талон ; б – схемы расположения арматуры в сечениях элементов стропильных конструкций

При успешной самостоятельной работе можно получить от ЭВМ в награду результаты автоматизированного статического расчета поперечной рамы для проектируемой по индивидуальному заданию колонны.

Пример армирования безраскосной фермы по результатам предыдущего расчета приведен на рисунке 26.

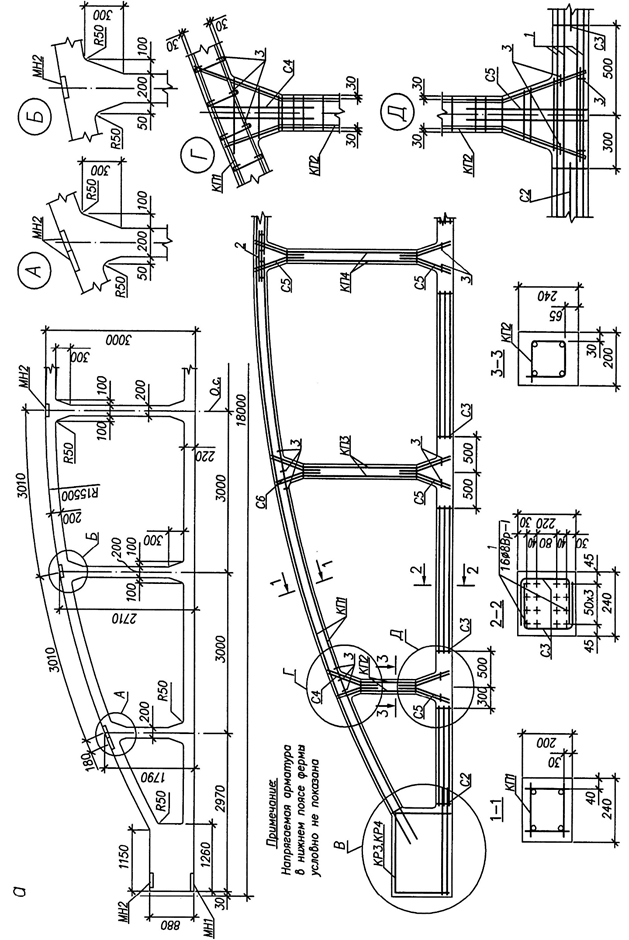
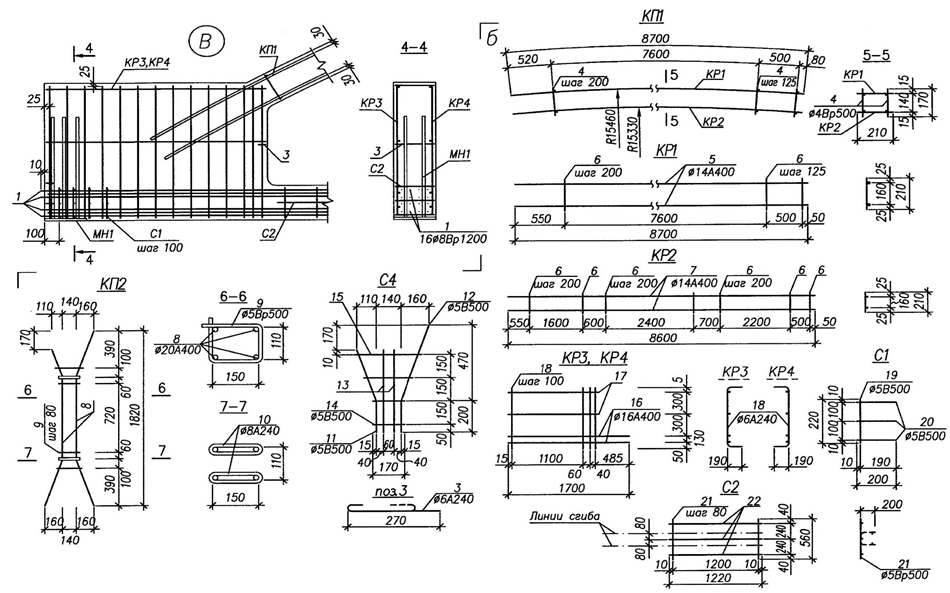
Рис. 26. Армирование безраскосной фермы:а – опалубочные размеры, сечения и схема армирования;

б – арматурные изделия

⇐ Предыдущая 1 2 34