Тема Элементы линейной алгебры»

«Тема Элементы линейной алгебры»

Карта-информатор по теме:

«СИСТЕМЫ ЛИНЕЙНЫХ НЕОДНОРОДНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ»

----

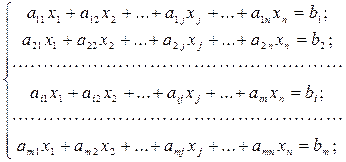
---- система m линейных уравнений с n переменными, где произвольные числа 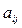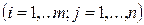- коэффициенты при переменных,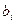 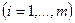- свободные члены уравнений.

Решением такой системы называется совокупность значений переменных х1, …, хn, при подстановке которых каждое уравнение системы обращается в верное равенство.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Две системы называются равносильными, если они имею одно и тоже множество решений.

Получают их с помощью элементарных преобразований:

1. изменение порядка уравнений в системе;

2. умножение или деление обеих частей любого уравнения системы на одно и то же неравное нулю число;

3. почленное сложение уравнений системы.

Рассматриваемую систему уравнений можно записать в матричной форм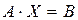е: , где

А – матрица коэффициентов при переменных, или матрица системы;

Х – матрица–столбец переменных;

В – матрица–столбец свободных членов, т.е.

; ; .

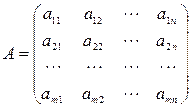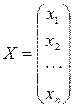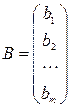Мы будем рассматривать системы, где m=n, т.е. количество уравнений в системе и количество входящих в них переменных равны. Тогда матрица А системы квадратная и имеет определитель 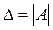, который называют определителем системы.

Такие системы можно решить одним из трех следующих методов:

1. метод Крамера;

2. матричный метод;

3. метод Гаусса.