Контакты

Случайная статья

Примеры и разбор решения заданий тренировочного модуля

Рассмотрим единичную окружность в прямоугольной системе координат хОу. (рис. 1)

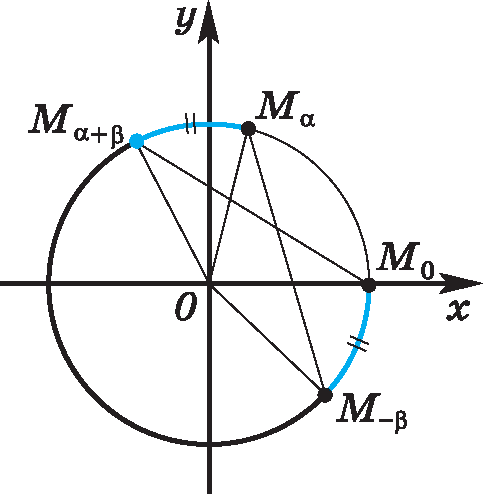
Рисунок 1 – единичная окружность

Точка 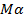получена поворотом точки Мₒ(1;0) на угол 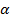, а точка 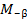на угол 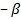и точка 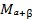на угол .

Углы 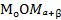и 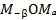равны, отрезки 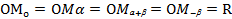. Значит, треугольник 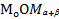равен треугольнику 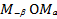, следовательно у них одинаковые стороны и .

Так как синус это ордината точки на единичной окружности, а косинус её абсцисса, то точки имеют координаты

;

;

).

Подставим координаты точек 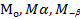и 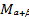в формулу для нахождения расстояния между ними. Получим:

.

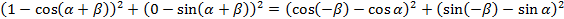Преобразуем левую часть, используя формулы квадрата суммы и разности двух выражений и тригонометрические тождества:

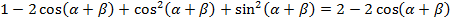
Преобразуем правую часть:

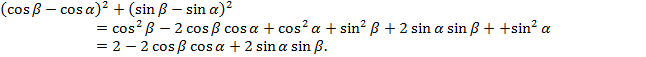
Соединим левую и правую части:

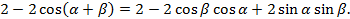
Разделим на 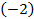каждое слагаемое :

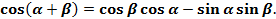
Получили формулу косинуса суммы.

Заменим и учтём, что 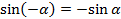, получим формулу косинуса разности

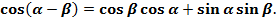
Докажем, что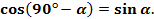

Так как 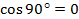, , 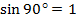то по формуле косинуса разности получаем:

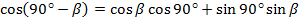
Заменим 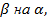получим

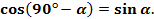
Так, например, 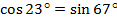, потому что .

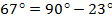Докажем, что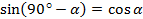

Подставим в формулу 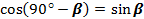значение 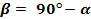, получим:

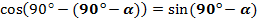
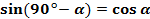
Для тангенса и котангенса тоже справедливы формулы

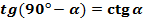
Выведем формулу синуса суммы и разности:

.

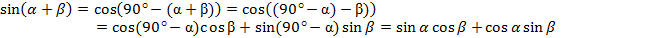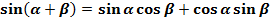
В этой формуле заменим и получим формулу синуса разности:

Для тангенса тоже есть формула суммы и разности. По определению .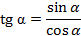

Тогда tg 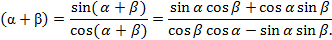, разделим числитель и знаменатель на

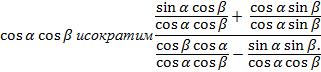
Получаем формулу тангенса суммы .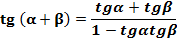

Заменим в ней и учтём, что tg⁡〖(-α)=〖-tg〗⁡α 〗, получим формулу тангенса разности

.

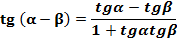Пример. Вычислим .

Для котангенса суммы и разности применяют формулы:

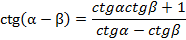
Примеры и разбор решения заданий тренировочного модуля

Пример 1. Найти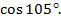

Решение: Представим 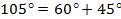, так как нам известны значения косинуса углов 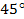и 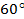Подставим в формулу косинуса суммы. Получаем:

.

Ответ: .

Пример 2. Найти .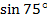

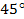Решение: Представим , так как нам известны значения синуса углов и 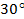Подставим в формулу синуса суммы. Получаем:

.

Ответ: .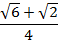

Пример 3. Вычислите .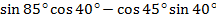

Решение: Применяем формулу синуса разности: .

Ответ: .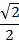

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.