
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определение:Функция F(x) называется первообразной для функции f(x) на промежутке I ,если для любого х из промежутка I выполняется равенство:
Определение:Функция F(x) называется первообразной для функции f(x) на промежутке I ,если для любого х из промежутка I выполняется равенство:
ИлиПервообразной для функции F(x) называется функция, производная которой равна данной.
Задача интегрирования состоит в том, чтобы для заданной функции найти все ее первообразные. Важную роль в решении этой задачи играетпризнак постоянства функции:
Если
на некотором промежутке I, то функция F - постоянная на этом промежутке.
Все первообразные функции а можно записать с помощью одной формулы, которую называют общим видом первообразных для функции f.
Основное свойство первообразных:
Любая первообразная для функции f на промежутке I может быть записана в виде
F(x) + C,
где F(x) – одна из первообразных для функции f(х) на промежутке I, а С – произвольная постоянная. В этом утверждении сформулированыдва свойства первообразной 1) какое бы число ни подставить вместо С, получим первообразную для f на промежутке I; 2) какую бы первообразную Ф для f на промежутке I ни взять, можно подобрать такое число С, что для всех х из промежутка I будет выполнено равенство Ф(х) = F(x) + C.
Основная задача интегрирования: записать все первообразные для данной функции. Решить её - значит представить первообразную в таком общем виде: F(x)+C
Таблица первообразных некоторых функций

Геометрический смысл первообразной
Графики первообразных -это кривые, получаемые из одной из них путём параллельного переноса вдоль оси ОУ
Примеры решения заданий
Пример 1. Выяснить, является ли функция F (x) = х 3 – 3х + 1 первообразной для функции f(x) = 3(х 2 – 1).
Решение:F'(x) = (х 3 – 3х + 1)′ = 3х 2 – 3 = 3(х 2 – 1) = f(x), т.е. F'(x) = f(x), следовательно, F(x) является первообразной для функции f(x).
Задание № 2 решить примеры после лекции
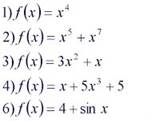
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|